Matematické Fórum

Filip2142 · 23. 04. 2017 19:43

Dobrý den,

mám tady jeden příklad se kterým si nevím úplně rady. Našel by se zde někdo, kdo by mi byl ochoten pomoci, či nasměrovat, jak daný příklad řešit? Děkuji moc, Filip.

//forum.matweb.cz/upload3/img/2017-04/69384_Podprostory.png

Avokado · 23. 04. 2017 20:57

v com vidis konkretny problem ?

v tomto priklade potrebujes overit z definicie ci dane mnoziny splnaju nejake podmienky.

vlado_bb · 23. 04. 2017 21:10

↑ Filip2142: Pripadne si vsimni diskusiu http://forum.matweb.cz/viewtopic.php?id=97684, tam sa riesi cosi podobne, len v jednoduchsom pripade.

Filip2142 · 23. 04. 2017 21:38

Nevím jak to obecně napsat a vyřešit dle definice :(

vlado_bb · 23. 04. 2017 21:47

↑ Filip2142: V prvom rade musis definicii poriadne porozumiet. Ak sa tak stane, tak okamzite UVIDIS, ze jedna z tych mnozin podpriestor je a druha nie je. Samotny dokaz bude potom uz iba technickym detailom.

Filip2142 · 27. 04. 2017 18:46

Tak vím o uzavřenosti na sčítání a násobení sklalárem, něco sem napíši, co jsem zatím napsal.

Filip2142

Tak vím o uzavřenosti na sčítání a násobení sklalárem, něco sem napíši, co jsem zatím napsal.

$1) M \neq \emptyset \nl 2) M \subset V \nl 3) \forall \vec x, \vec y \in M: \vec x + \vec y \in M \nl 4) \forall \vec x \in M, \forall \alpha \in T : \alpha \cdot \vec x \in M$

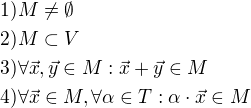
Nechť máme vektory 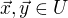$\vec x, \vec y \in U$
$1) \vec x + \vec y = (a_2x^2 + a_1x + a_0 ) + (b_2x^2 + b_1x + b_0) = (a_2 + b_2)x^2 + (a_1 + b_1)x + (a_0+b_0)$
ale protože 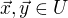$\vec x, \vec y \in U$ , potom pro čísla 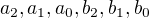$a_2,a_1,a_0,b_2,b_1,b_0$ , platí:
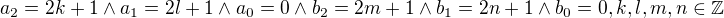$a_2 = 2k+1 \wedge a_1 = 2l+1 \wedge a_0 = 0 \wedge b_2 = 2m+1 \wedge b_1 = 2n+1 \wedge b_0 = 0, k,l,m,n \in \mathbb{Z}$ , potom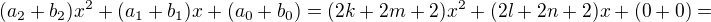

$(a_2 + b_2)x^2 + (a_1 + b_1)x + (a_0+b_0) = (2k + 2m + 2)x^2 + (2l + 2n + 2)x + (0 + 0) =$

A dále nevím, jak to formálně dopsat, vím, že pro daný daný výsledek musí být první dva koeficienty liché (aby splňoval uzavřenost na sčítání), což výsledek nebude splňovat, ale jak to zapsat.
$U$ není uzavřená na sčítání.

vlado_bb · 27. 04. 2017 19:13

↑ Filip2142: Ides na to dobre, ale prilis si komplikujes zivot. Ukazme si to na jednoduchsom priklade. Majme taketo tvrdenie:

Kazde prvocislo je mensie ako 40.

Toto samozrejme nie je pravda. Ako by si ma o tom presvedcil?

Filip2142 · 27. 04. 2017 19:15

Tak protidůkazem a našel bych prvočíslo větší než 40. Napadlo mě také vzít si (vyrobit) dva vektory s danými parametry a dokázat to již na příkladě, že to neplatí (lichost), ale nevím jestli to bude dostatečné.

vlado_bb · 27. 04. 2017 19:21

↑ Filip2142: A preco pochybujes? Vazne ma to zaujima, z urcitych dovodov. Preco pochybujes, ze ak mi ukazes, ze 41 je prvocislo, tak to nestaci na to, aby bolo moje tvrdenie vyvratene?

Filip2142

Takhle, tohle je jeden z mnoha příkladů, které mám dokázat, ale otázka je, jestli to bude stačit učiteli o nic víc mi nejde, i když mě teď napadá, že bych to mohl dodělat takto:

že se to rovná:

$= (2(k+m)+2)x^2 + (2(l+n)+2)\cdot x + 0 = \nl = c_2x^2 + c_1x + c_0 \nl c_2 = 2s + 2\wedge c_1=2r + 2\wedge c_0 = 0,\;\;\; r,s \in \mathbb{Z}$
Ale již to nesplňuje podmíněné vlastnosti koeficientů, to by také šlo ne?

vlado_bb

↑ Filip2142: Ok, pomozem ti s tvojou ulohou, ale aj ty mi pomoz s mojim matematicko-psychologickym vyskumom. Takze, mame tvrdenie, ze vsetky prvky istej mnoziny maju nejaku vlastnost. Co ta vedie k nazoru, ze ak najdes jeden prvok tej mnoziny, ktory tu vlastnost nema, tak to nestaci k tomu, aby bolo jasne, ze tvrdenie nebolo pravdive?

Filip2142 · 27. 04. 2017 19:38

Jako důkaz to stačí :), já jsem to chtěl napsat více v definicích. Určitě netvrdím, že to nestačí to ne :) Jinak ten zápis jsem už opravil že C2 = 2s + 2 a apod. což lze takto dokázat také a stačilo by to ne?

vlado_bb

↑ Filip2142: A ak to teda ako dokaz podla teba staci, preco sa snazis dostat tam co najviac symbolov, premennych a operacii? Zda sa ti to viac "matematicke"? Alebo v kutiku dusi si stale neveris, ze uviest jeden konkretny protipriklad nestaci? Budem velmi rad, ak sa pokusis co najpresnejsie popisat svoje myslienky, dakujem.

A k ulohe sa vratim, slubujem.

Teda k tym prvocislam ... zda sa ti dokaz "41 je prvocislo vacsie ako 40" nejako menej hodnotny ako taky, kde vystupuje vela premannych, operacii a inych zlozitosti?

Filip2142 · 27. 04. 2017 19:43

Ano máš pravdu, tvá druhá intuice je správná. +Raději to dělám matematicky (definicky), abych si zvykl na důkazy apod. Nic víc hele :) Asi tam uvedu i protipříklad, abych měl jistotu :D

vlado_bb · 27. 04. 2017 19:46

↑ Filip2142: Tak teda podme naspat k ulohe. Napis mi prosim co najjedoduchsi prvok mnoziny $U$ .

Filip2142 · 27. 04. 2017 19:48

$3x^{2} + 3x^{1}$

vlado_bb · 27. 04. 2017 19:49

↑ Filip2142: Este jednoduchsi skus ... 3 je prilis velke cislo.

Filip2142 · 27. 04. 2017 19:52

Jo, jasně patří do celých čísel tak: $x^{2} + x$

vlado_bb · 27. 04. 2017 19:53

↑ Filip2142: Fajn, tak teraz tie dva prvky, co si nasiel, scitaj a urob z toho zaver a potom este pockaj na moju odpoved.

Filip2142 · 27. 04. 2017 19:55

$4x^{2}+4x$ , neplatí nutná lichost a to stačí, dle mě

vlado_bb · 27. 04. 2017 20:02

↑ Filip2142: Presne. Ak mame vyvratit taketo tvrdenie, staci jediny protipriklad. Lubovolny, ale ista matematicka kultura nam kaze vybrat co najjednoduchsi protipriklad. Preto by mojim riesenim bol polynom 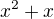$x^2+x$ , ktory scitam sam so sebou a dostanem $2x^2+2x$ . A k tomu, o co si sa pokusal predtym, teda o cosi "vseobecne", kde si mal premenne $k,l,m,n,c_0, \dots, c_2$ asi tolko - toto je pomerne casty pristup mnohych studentov, ktori zastavaju nazor "cim zlozitejsie, tym viac matematika". V skutocnosti si tym ale iba skodis, pretoze davas najavo, ze ti veci vobec nie su jasne. Pravda je taka, ze "cim jednoduchsie, tym lepsia matematika".

Filip2142 · 27. 04. 2017 20:04

Jasný dám na tebe ;). Jeden doktorand právě tvrdil, že by to takto neuznal, tak jsem si nebyl úplně jistý...

vlado_bb · 27. 04. 2017 20:05

↑ Filip2142: Doktorand v matematickom odbore? Nech sa mi ozve :)

Filip2142 · 27. 04. 2017 20:08

Nevím, jak se jmenuje :D. Říkala mi to kamarádka, která s ním konzultovala obdobný příklad. Jinak kdybych ještě vyšetřoval to násobení skalárem, i když to už není potřeba.

Vynásobit nějakým R číslem, např. 1/2 a ukázat, že koeficient nepatří do celých čísel ano?

Matematické Fórum

#1 23. 04. 2017 19:43

Jsou dané množiny podprostory?

#2 23. 04. 2017 20:57

Re: Jsou dané množiny podprostory?

#3 23. 04. 2017 21:10

Re: Jsou dané množiny podprostory?

#4 23. 04. 2017 21:38

Re: Jsou dané množiny podprostory?

#5 23. 04. 2017 21:47

Re: Jsou dané množiny podprostory?

#6 27. 04. 2017 18:46

Re: Jsou dané množiny podprostory?

#7 27. 04. 2017 19:10 — Editoval Filip2142 (27. 04. 2017 19:13)

Re: Jsou dané množiny podprostory?

#8 27. 04. 2017 19:13

Re: Jsou dané množiny podprostory?

#9 27. 04. 2017 19:15

Re: Jsou dané množiny podprostory?

#10 27. 04. 2017 19:21

Re: Jsou dané množiny podprostory?

#11 27. 04. 2017 19:29 — Editoval Filip2142 (27. 04. 2017 19:36)

Re: Jsou dané množiny podprostory?

#12 27. 04. 2017 19:33 — Editoval vlado_bb (27. 04. 2017 19:33)

Re: Jsou dané množiny podprostory?

#13 27. 04. 2017 19:38

Re: Jsou dané množiny podprostory?

#14 27. 04. 2017 19:41 — Editoval vlado_bb (27. 04. 2017 19:44)

Re: Jsou dané množiny podprostory?

#15 27. 04. 2017 19:43

Re: Jsou dané množiny podprostory?

#16 27. 04. 2017 19:46

Re: Jsou dané množiny podprostory?

#17 27. 04. 2017 19:48

Re: Jsou dané množiny podprostory?

#18 27. 04. 2017 19:49

Re: Jsou dané množiny podprostory?

#19 27. 04. 2017 19:52

Re: Jsou dané množiny podprostory?

#20 27. 04. 2017 19:53

Re: Jsou dané množiny podprostory?

#21 27. 04. 2017 19:55

Re: Jsou dané množiny podprostory?

#22 27. 04. 2017 20:02

Re: Jsou dané množiny podprostory?

#23 27. 04. 2017 20:04

Re: Jsou dané množiny podprostory?

#24 27. 04. 2017 20:05

Re: Jsou dané množiny podprostory?

#25 27. 04. 2017 20:08

Re: Jsou dané množiny podprostory?

Zápatí