Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » integrovateľná neklesajúca funkcia na neohraničenom intervale (TOTO TÉMA JE VYŘEŠENÉ)
#2 16. 07. 2017 16:32
- van Thomas

- Příspěvky: 61
- Škola: FAV ZČU
- Reputace: 5
Re: integrovateľná neklesajúca funkcia na neohraničenom intervale
Ahoj, myslím, že platí. Navíc předpoklad 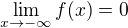 je podle mě zbytečný, protože
je podle mě zbytečný, protože  .
.
Offline
#3 16. 07. 2017 16:58 — Editoval van Thomas (16. 07. 2017 17:01)
- van Thomas

- Příspěvky: 61
- Škola: FAV ZČU
- Reputace: 5
Re: integrovateľná neklesajúca funkcia na neohraničenom intervale
Možná to jde elegantněji pomocí nějakého kritéria, ale dokazoval bych to sporem. Není-li  , pak existuje
, pak existuje  a posloupnost
a posloupnost 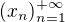 záporných čísel taková, že
záporných čísel taková, že 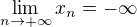 a
a 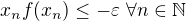 . Navíc jistě není problém posloupnost zvolit tak, aby
. Navíc jistě není problém posloupnost zvolit tak, aby 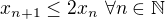 , tj.
, tj.  . Potom pro libovolné
. Potom pro libovolné 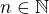 platí
platí 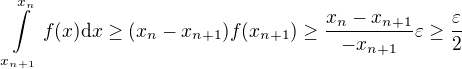 . Odtud
. Odtud 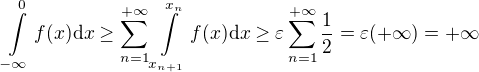 .
.
Offline
#4 16. 07. 2017 19:07 — Editoval jarrro (16. 07. 2017 19:17)
Re: integrovateľná neklesajúca funkcia na neohraničenom intervale
Díky↑ van Thomas:
Využil si niekde neklesajúcosť? Podľa dôkazu to vyzerá, že by to prešlo pre nezáporné funkcie . Je to tak?
MATH IS THE BEST!!!
Offline
#5 16. 07. 2017 19:19
- van Thomas

- Příspěvky: 61
- Škola: FAV ZČU
- Reputace: 5
Re: integrovateľná neklesajúca funkcia na neohraničenom intervale
Využil v tom prvním odhadu integrálu, bez monotonie to neprojde :)
Offline
#6 16. 07. 2017 19:24
Re: integrovateľná neklesajúca funkcia na neohraničenom intervale
↑ van Thomas:aha fakt. dík označím za vyriešené.
MATH IS THE BEST!!!
Offline
#7 17. 07. 2017 00:29
Re: integrovateľná neklesajúca funkcia na neohraničenom intervale
↑ jarrro:
Není-li  , pak z monotonnosti funkce
, pak z monotonnosti funkce  a
a  plyne, že existuje
plyne, že existuje  takové, že platí
takové, že platí  pro dostatečně malá záporná
pro dostatečně malá záporná  , tj.
, tj.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#9 17. 07. 2017 14:12
- van Thomas

- Příspěvky: 61
- Škola: FAV ZČU
- Reputace: 5
Re: integrovateľná neklesajúca funkcia na neohraničenom intervale
↑ Pavel:
Dovolím si nesouhlasit. Jako protipříklad vezměme funkci 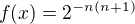 pro
pro ![kopírovat do textarea $x\in(x_{n+1},x_n]$](/mathtex/a4/a458ed3cb0df8387603e4613e3ffeed4.gif) , kde
, kde  ,
, 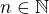 , a
, a  pro
pro ![kopírovat do textarea $x\in(-1,0]$](/mathtex/1c/1c700859c4edf5cc6bc0ec87c3d7d846.gif) . Evidentně
. Evidentně 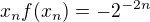 ,
, 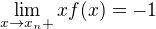 ,
, 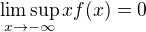 ,
, 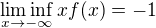 . Tj.
. Tj. 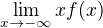 neexistuje (není
neexistuje (není  ),
),  je neklesající, ale
je neklesající, ale  není na žádném okolí
není na žádném okolí  shora omezená záporným číslem. Nicméně platí
shora omezená záporným číslem. Nicméně platí 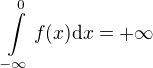 , jak jsem obecně dokázal výše.
, jak jsem obecně dokázal výše.
Offline
#10 17. 07. 2017 14:59
Re: integrovateľná neklesajúca funkcia na neohraničenom intervale
↑ van Thomas:
Funkcia 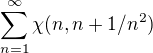 (sucet charak. funkcii intervalov) ma vlastny integral
(sucet charak. funkcii intervalov) ma vlastny integral  , ale nema limitu. Plati ale, ze ak ma funkcia limitu
, ale nema limitu. Plati ale, ze ak ma funkcia limitu 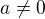 , potom nema vlastny integral, lebo je
, potom nema vlastny integral, lebo je  pre
pre  .
.
Offline
#11 17. 07. 2017 15:29
- van Thomas

- Příspěvky: 61
- Škola: FAV ZČU
- Reputace: 5
Re: integrovateľná neklesajúca funkcia na neohraničenom intervale
↑ Xellos:
Nevím přesně, na co to má být reakce, ale bavíme se tu o monotónních funkcích :)
Offline
#12 17. 07. 2017 17:18 — Editoval jarrro (09. 11. 2019 21:44)
Re: integrovateľná neklesajúca funkcia na neohraničenom intervale
↑ Pavel:↑ van Thomas: myslím, že to súvisí s tým, že o súčine neklesajúcich funkcií s rôznymi znamienkami sa nedá nič povedať
napríklad aj je taký divný prípad keď  je dokonca klesajúca na okolí mínus nekonečna
je dokonca klesajúca na okolí mínus nekonečna
MATH IS THE BEST!!!
Offline
#13 17. 07. 2017 17:29
- van Thomas

- Příspěvky: 61
- Škola: FAV ZČU
- Reputace: 5
Re: integrovateľná neklesajúca funkcia na neohraničenom intervale
↑ jarrro:
Přesně tak, kdybychom věděli (předpokládali), že je  monotónní, šel by samozřejmě důkaz zjednodušit, ale nevíme.
monotónní, šel by samozřejmě důkaz zjednodušit, ale nevíme.
Offline
#14 17. 07. 2017 22:39 — Editoval Xellos (17. 07. 2017 22:40)
Re: integrovateľná neklesajúca funkcia na neohraničenom intervale
↑ van Thomas:
Bola to reakcia na  .
.
Ok, vyzeralo ze to myslis vseobecne.
Offline
#15 19. 07. 2017 00:18 — Editoval Pavel (19. 07. 2017 00:20)
Re: integrovateľná neklesajúca funkcia na neohraničenom intervale
↑ van Thomas:
Souhlasím s Tvým postřehem. Můj postup by fungoval v případě, že by platilo  . To, zda je funkce
. To, zda je funkce  monotonní, ve skutečnosti nehraje žádnou roli, byť jsem tuto skutečnost omylem zmínil.
monotonní, ve skutečnosti nehraje žádnou roli, byť jsem tuto skutečnost omylem zmínil.
Uvedu ještě jeden důkaz, který kopíruje obdobné tvrzení z teorie nekonečných řad.
Nechť 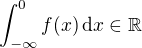 a
a  je neklesající. Pak pro libovolné
je neklesající. Pak pro libovolné  existuje
existuje  , takové že pro libovolná reálná
, takové že pro libovolná reálná 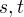 splňující nerovnost
splňující nerovnost  platí
platí  .
.
Volme  a
a 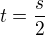 . pak
. pak  . Funkce
. Funkce  je neklesající, proto platí
je neklesající, proto platí  , kde
, kde ![kopírovat do textarea $x\in\left[s,\frac s2\right]$](/mathtex/9c/9c647c27194bc561b0d3f76d85e48fce.gif) . Kombinací všech uvedených skutečnosti odvodíme diskutovanou limitu, tj.
. Kombinací všech uvedených skutečnosti odvodíme diskutovanou limitu, tj.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » integrovateľná neklesajúca funkcia na neohraničenom intervale (TOTO TÉMA JE VYŘEŠENÉ)
 ?
?