Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 18. 06. 2009 16:23 — Editoval Marian (18. 06. 2009 17:51)
Třetí mocnina
Dokažte, že pro všechna přirozená čísla  existuje přirozené číslo
existuje přirozené číslo  takové, že platí
takové, že platí  .
.
Pozn.: Váhal jsem, zda-li to nepatří do zajímavých středoškolských úloh, ale nakonec jsem umístil tuto úlohu sem.
:-)
Editováno!
Offline
#2 18. 06. 2009 17:31 — Editoval Pavel (18. 06. 2009 17:53)
Re: Třetí mocnina
↑ Marian:
Mě to vychází už od 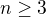 :-)
:-)
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#3 18. 06. 2009 17:53 — Editoval Marian (18. 06. 2009 18:02)
Re: Třetí mocnina
↑ Pavel:
Změnil jsem v zadání neostré znaky nerovnosti za ostré. Pak už ti to neprojde. Chce to důkaz (samozřejmě mezi tagy hide a /hide).
PS: Vidím již tvoje řešení. Souhlasím! Moje řešení využívalo platnosti nerovnosti
Offline
#4 18. 06. 2009 18:13
Offline
#5 18. 06. 2009 18:22
Re: Třetí mocnina
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#6 18. 06. 2009 18:31
Re: Třetí mocnina
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#7 18. 06. 2009 18:50
Offline
#8 13. 10. 2009 13:12
- mcgilikady
- Zelenáč
- Příspěvky: 3
- Reputace: 0
Re: Třetí mocnina
↑ mcgilikady:
pro vysvětlění mé myšlenky. m přeci nemůže být stejné číslo pro všechna n je větší než 10. jaké by tedy dle vás mělo být m aby to sedělo pro všechna n je větší než 10. nesmysl.
Offline
#9 13. 10. 2009 13:14
- mcgilikady
- Zelenáč
- Příspěvky: 3
- Reputace: 0
Re: Třetí mocnina
pro vysvětlění mé myšlenky. m přeci nemůže být stejné číslo pro všechna n je větší než 10. jaké by tedy dle vás mělo být m aby to sedělo pro všechna n je větší než 10. nesmysl. opavte mě jestli se pletu a zkus si tam dosadit za n jednou 10 a jednou 100000 a m v tom případě se musí lišit...
Offline
#10 13. 10. 2009 13:30
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Třetí mocnina
↑ mcgilikady:
m skutečně nemůže být stejné pro všechny n. Ale to se ani nepožaduje. To by muselo zadání znít takto:
Dokažte, že existuje přirozené číslo  takové, že pro všechna přirozená čísla
takové, že pro všechna přirozená čísla  platí
platí  .
.
Offline
 , pak se snadno ukáže, že pro
, pak se snadno ukáže, že pro  platí
platí  .
.  a
a  je to
je to 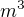
 a
a  je to
je to  a
a  je to
je to  je to
je to 
 a
a  je to
je to  a
a  je to
je to  je to
je to 
 a
a  je to
je to  a
a 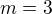 . To, že nerovnost platí i pro
. To, že nerovnost platí i pro  , se lehce ověří.
, se lehce ověří.![kopírovat do textarea $\lceil\sqrt[3]{n}\rceil\le\lfloor\sqrt[3]{3n}\rfloor$](/mathtex/d5/d580b4db4916e499c896beba267a85b7.gif)
![kopírovat do textarea $ f(x):=\lfloor\sqrt[3]{3x}\rfloor -\lceil\sqrt[3]{x}\rceil, \qquad x\in\mathbb{R}, $](/mathtex/be/be4cb473843b33169d2a547f6f3daf72.gif)
![kopírovat do textarea $m\in \langle\sqrt[3]{n};\sqrt[3]{3}\sqrt[3]{n}\rangle$](/mathtex/33/335b2fc59fcc4e28c7ee4686019047b7.gif) a keď je n viac ako 10 tak je ten interval dlhší ako 1,preto obsahuje aj prirodzené číslo. pre n=10 ľahko nahliadneme,že m=3
a keď je n viac ako 10 tak je ten interval dlhší ako 1,preto obsahuje aj prirodzené číslo. pre n=10 ľahko nahliadneme,že m=3
 . Chcem ukázať, že v tomto leží tretia mocnina nejakého prirodzeného m. Potom ale
. Chcem ukázať, že v tomto leží tretia mocnina nejakého prirodzeného m. Potom ale ![kopírovat do textarea $m\in(\sqrt[3]{n},\sqrt[3]{3n})$](/mathtex/13/13d57ac8253632e193d11b8540b5227e.gif) . Stačí preto ukázať, že
. Stačí preto ukázať, že ![kopírovat do textarea $\left\lfloor\sqrt[3]{n}\right\rfloor<\left\lfloor\sqrt[3]{3n}\right\rfloor$](/mathtex/77/77c24b05d51f9d013df4f3aeca1e418b.gif)
![kopírovat do textarea $\left\lfloor\sqrt[3]{n}\right\rfloor\ge\left\lfloor\sqrt[3]{3n}\right\rfloor$](/mathtex/30/30dc8143c674aa864ea5c5edaaac43f2.gif) . Keďže
. Keďže ![kopírovat do textarea $\forall n\in\mathbb{N}\,:\;\sqrt[3]{n}<\sqrt[3]{3n}$](/mathtex/50/50c35b0c9939204ae4a9c16c8dd45f30.gif) , vzťah
, vzťah  pre dolné celé časti nastať nemôže. Teraz predpokladajme, že platí rovnosť, teda
pre dolné celé časti nastať nemôže. Teraz predpokladajme, že platí rovnosť, teda![kopírovat do textarea $\left\lfloor\sqrt[3]{n}\right\rfloor=\left\lfloor\sqrt[3]{3n}\right\rfloor$](/mathtex/7a/7acae8391c33f5ac4098532add136d9b.gif)
![kopírovat do textarea $\varphi\,:\;\mathbb{R}^+\to\mathbb{R}^+\,,\;\varphi(x)=\sqrt[3]{3x}-\sqrt[3]{x}$](/mathtex/2d/2dc32e39474cad02af43f3bcda7663e8.gif)
 existuje ľubovoľne veľké číslo
existuje ľubovoľne veľké číslo  tak, že
tak, že![kopírovat do textarea $\sqrt[3]{n}<k<\sqrt[3]{3n}$](/mathtex/88/88553474e774bd4e6733b355f8f18094.gif)
![kopírovat do textarea $\sqrt[3]{3n}-\sqrt[3]{n}>1$](/mathtex/50/50c767becc09d7722d969e42da4ac816.gif) . Pre ten zvyšok
. Pre ten zvyšok  by som to snáď dotiahol nejako numericky.
by som to snáď dotiahol nejako numericky.