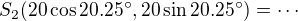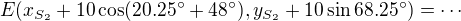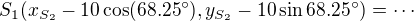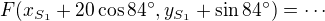Matematické Fórum

Rufus · 04. 11. 2017 11:00 — Editoval Rufus (04. 11. 2017 11:02)

Zdravím, prosím o pomoc výpočtu tečny složeného oblouku. Jak se vypočítá délka tečny 12,92, případně 16,17?

//forum.matweb.cz/upload3/img/2017-11/89492_slo%25C5%25BEen%25C3%25BD_oblouk.png

Přes gonio funkce jsem přišel na hodnoty přepony tečny 1. oblouku - 2,88 a 2. oblouku - 4,62, ale nevím jak přijít na 3. oblouku.

x1 = 2,77/cos15,75° = 2,88
x2 = 4,45/cos15,75° = 4,62

Předem děkuji za pomoc.

Jj · 05. 11. 2017 06:54 — Editoval Jj (05. 11. 2017 08:58)

↑ Rufus:

Dobrý den.

Možná na to jít z druhé strany:

- goniometricky spočítat R1, R2, R3
- zvolit kartézskou soustavu souřadnic (střed ve středu oblouku 3, osa x v pravém rameni výseče 3)
- postupně spočítat souřadnice středů oblouků 2, 3 a souřadnice hraničních bodů oblouků 2, 3
- sestavit rovnice tečen 12,92 a 16,17
- spočítat souřadnice průsečíků tečen a hledané délky

Rufus · 05. 11. 2017 12:49

↑ Jj:
děkuji za pomoc, ale i tak mi to nepomohlo :/

Jj · 05. 11. 2017 13:19

↑ Rufus:

A proč? Podařilo se něco? Nebo je rada mimo?

Rufus · 06. 11. 2017 18:54

↑ Jj:
Nepodařilo se - nevím jak :(

Jj · 06. 11. 2017 20:53

↑ Rufus:

Řekl bych - o výpočet poloměrů R1 - R3 jste se pokusit mohl.

V každé kruhové výseči je možno vymezit pravoúhlý trojúhelník s odvěsnami danými

- poloměrem (např. R1),
- úsekem tečny v krajním bodě příslušného oblouku (např. úsek o tečny o délce 2,77)

a s přeponou půlící středový úhel dané výseče (tzn. jeden z ostrých úhlů trojúhelníku = polovině středového úhlu výseče; např. úhel 15,75 : 2 = 7,875°).

K vlastnímu výpočtu se hodí např. funkce kotangens, tangens.