Matematické Fórum

liamlim

Ahoj! Mám rychlý dotaz. Je připuštěno operace s množinami definovat rekurzivně? Ptám se, jestli by bylo kupříkladu korektní v nějaké teorii množin v určitém z axiomů použít operaci definovanou způsobem:

$(\forall a)(\forall b)(a\to b\Leftrightarrow a\in b\lor (\exists c)(a\to c\land c\to b))$

Díky!

Rumburak

↑ liamlim:

Ahoj. Nemám sice přehled přes všechny existující teorie množin, kdysi jsem trochu studoval
jen základy teorie Zelmello-Fraenkelovy a teorie Goedel-Bernaysovy. Ale pokud má formule

$(\forall a)(\forall b)(a\to b\Leftrightarrow a\in b\lor (\exists c)(a\to c\land c\to b))$

sloužit za definici symbolu $a\to b$ , tak se obávám, že by to neprošlo v žádné TM.
Ale třeba se pletu.

Je to hlavně otázka logiky: má formule $a\in b\lor (\exists c)(a\to c\land c\to b)$ smysl i
v případech, kdy ještě nevíme nic o symbolu (resp. relaci) $x \to y$ ?

Myslím, že by Tě mohla zajímat konstrukce na principu tansfinitní indukce, která tento
problém rekursivních definic řeší.

liamlim · 08. 11. 2017 15:53

↑ Rumburak:

Díky. Ještě jedná kratičká otázka. Je možné, aby bylo v nějakém tvrzení použito $\exists\varphi$ ? Například je možné, aby teorie obsahovala axiom: $(\forall a)(\exists\varphi)(a = \{x\mid\varphi(x)\})$ , kde $\{x\mid\varphi(x)\}$ již je korektně definováno pro libovolnou formuli $\varphi$ ?

liamlim

Taky by mě zajímalo, jestli je přípustné uvažovat něco jako skupinu formulí. $(\forall\varphi)(\varphi\,\mathrm{is\,ok}\lor \neg\varphi\,\mathrm{is\,ok})$

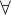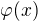Edit: A jestli by v nějaké teorii prošlo předpokládat, že všechny formule vyskytující se u $\forall$ a $\exists$ mají právě jednu volnou proměnnou, aby $\varphi(x)$ dávalo dobrý smysl.

check_drummer · 08. 11. 2017 16:08

↑ liamlim:
Ahoj, myslím, že to není možné použít, protože není určeno podle čeho ta rekurze probíhá. Každá rekurze probíhá podle nějakého ordinálu, ne? Asi by se musela definovat relace šipka s argumentem ordinálu.. A šipka bez argumentu by se definovala tak, že pro nějaký ordinál x platí šipka s argumentem x.

liamlim

Totiž tak. Já jsem se zase zamyslel v tramvaji (ach jo :D) a napadlo mě něco takového:

Definoval bych:
$(\forall\varphi)(\forall\psi):\{\varphi\} = \{\psi\}:= (\forall a)(\varphi(a)\Leftrightarrow\psi(a))$
$(\forall\varphi)(\forall a): a\in\{\varphi\}:= \varphi(a)$

Kde bych tedy předpokládal, že $\forall\varphi$ a $\forall\varphi$ vždy odpovídá formuli s jednou volnou proměnnou. Samozřejmě máme i konstantní nepravdivou formuli, které by odpovídala prázdná množina. To je všechno ale nějaké divné a vůbec nevím, jestli matematika nějaké takové manipulace s formulemi připouští.

Edit: Ty závorky $\{\}$ by vlastně jen převedly formule k jejich množinovému protějšku

EDIT: Proč tu nejde napsat sekcenci (dolar)(lomírko){(dolar)? Chtěl jsem v latexovém zápisu zapsat jen jednu složenou závorku a byla to chyba. Kulatá závorka zapsat lze: $($

EDIT3: Tady přece nejsou žádné axiomy, ne? Jsou to všechno objekty definice z predikátové logiky. Neměl by tam tedy být žádný spor, ne?

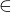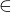Poslední edit: Ono by ani nebylo možné definovat slavnou množinu $\{x\mid x\notin x\}$ , neboť na začátku máme jen všechny existující formule s jednou volnou proměnnou. Vůbec nevíme, co nějaký symbol $\in$ znamená. Až poté jej definujeme s pomocí jakési formule $\varphi$ , která ale o nějakém $\in$ vůbec neví! Až s pomocí existující formule $\varphi$ definujeme novou formuli $\psi(x) = x\in\{\varphi\}$ . Nikdy ale nemůžeme definovanou funkci použít v její definici, protože o ní ještě nevíme.

vanok · 08. 11. 2017 20:55

Poznamka.
Mozno by bolo uzitocne zacat so serioznym citanim dobrej knihy z teorie mnozin.
Napr. kniha T. Jech, Set theory moze byt uzitocna.

Rumburak

↑ liamlim:

Ahoj.

Domnívám se , že ani to není možné. Napíšeme-li $\forall x$ resp. $\exists x$ ,
pak se předpokládá, že $x$ je některý ze studovaných objektů (zpravidla prvek
nějaké dohodnuté množiny či třídy, například číslo nebo číselná množina),
avšak nikoli formule, která patří pouze do jazyka, jímž se o množinách a jejich prvcích
hovoří, při čemž sama mezi tyto objeky nepatří.
Tato "dvojvrstevnost", která zkoumané objeky odděluje od formulí, jimž je o nich
vypovídáno, je nutná. Experti přes logiku by k tomu jistě řekli více.

PS.

Na "vizitce" máš uvedeno, že studuješ MFF UK. Mohu se zeptat, který obor a ročník?
Za mých studií oboru matematika se teorie množin probírala už v prvním ročníku, zatímco
matematická logika překvapivě až v pátém, ale nejspíše k tomu nějaké důvody byly.

Také máš možnost využít kosultačních hodin svých učitetlů.

Matematické Fórum

#1 08. 11. 2017 12:56 — Editoval liamlim (08. 11. 2017 12:58)

teorie množin, rekurzivní definice

#2 08. 11. 2017 13:36 — Editoval Rumburak (09. 11. 2017 10:49)

Re: teorie množin, rekurzivní definice

#3 08. 11. 2017 15:53

Re: teorie množin, rekurzivní definice

#4 08. 11. 2017 16:03 — Editoval liamlim (08. 11. 2017 16:04)

Re: teorie množin, rekurzivní definice

#5 08. 11. 2017 16:08

Re: teorie množin, rekurzivní definice

#6 08. 11. 2017 16:20 — Editoval liamlim (08. 11. 2017 16:52)

Re: teorie množin, rekurzivní definice

#7 08. 11. 2017 20:55

Re: teorie množin, rekurzivní definice

#8 09. 11. 2017 11:16 — Editoval Rumburak (09. 11. 2017 12:14)

Re: teorie množin, rekurzivní definice

Zápatí