Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » Lineární rovnice s absolutní hodnotou-slozite (TOTO TÉMA JE VYŘEŠENÉ)
#3 09. 01. 2008 23:05
Re: Lineární rovnice s absolutní hodnotou-slozite
rozeberu ten prvni priklad, ostatni jsou analogicke. resme tedy  . nejdrive se budeme zabyvat tou vnitrni absolutni hodnotou
. nejdrive se budeme zabyvat tou vnitrni absolutni hodnotou  , ktera nabyva nulove hodnoty pro
, ktera nabyva nulove hodnoty pro 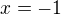 . Rozdelme tedy reseni na dve casti A a B takto: cast A na intervalu
. Rozdelme tedy reseni na dve casti A a B takto: cast A na intervalu  a cast B na intervalu
a cast B na intervalu  . zabyvejme se nejdrive casti A: argument absolutni hodnoty pro
. zabyvejme se nejdrive casti A: argument absolutni hodnoty pro  nabyva zapornych hodnot, ziskame tedy rovnici
nabyva zapornych hodnot, ziskame tedy rovnici  . nyni je nutne vysetrit absolutni hodnotu
. nyni je nutne vysetrit absolutni hodnotu  , jejiz nulovy bod je
, jejiz nulovy bod je  . rozdelme reseni na podcasti C a D takto: cast C na intervalu
. rozdelme reseni na podcasti C a D takto: cast C na intervalu  a cast D na intervalu
a cast D na intervalu  . pro interval C ziskame rovnici
. pro interval C ziskame rovnici  , coz dava koren
, coz dava koren  . nyni musime overit, zda-li je tento koren skutecne korenem puvodni rovnice, tedy musi platit
. nyni musime overit, zda-li je tento koren skutecne korenem puvodni rovnice, tedy musi platit  , cemuz koren
, cemuz koren  vyhovuje. nyni se vratime na interval D, kde resime rovnici
vyhovuje. nyni se vratime na interval D, kde resime rovnici  , coz dava reseni
, coz dava reseni  vyhovujici puvodni rovnici. ted se vratime zpet na interval B, kde resime rovnici
vyhovujici puvodni rovnici. ted se vratime zpet na interval B, kde resime rovnici  . nulovy bod teto absolutni hodnoty je
. nulovy bod teto absolutni hodnoty je  , reseni nyni opet rozdelime na intervaly E:
, reseni nyni opet rozdelime na intervaly E:  a interval F:
a interval F:  . na intervalu E resime rovnici
. na intervalu E resime rovnici  , jejiz reseni
, jejiz reseni  je opet resenim puvodni rovnice. to stejne provedu jeste pro interval F: resim rovnici
je opet resenim puvodni rovnice. to stejne provedu jeste pro interval F: resim rovnici  , reseni
, reseni  opet vyhovuje puvodni rovnici. timto postupem jsme tedy nasli vsechna reseni
opet vyhovuje puvodni rovnici. timto postupem jsme tedy nasli vsechna reseni  .
.
Offline
#4 09. 01. 2008 23:21 — Editoval jelena (09. 01. 2008 23:23)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Lineární rovnice s absolutní hodnotou-slozite
|3-|2-x||<=2x
Nulove body - resim rovnici:
3-|2-x|=0
3=|2-x| tady si jen predstavim, co by mohlo byt misto x, aby absolutni hodnota byla 3
Nulove body -1, 5
Ted si vytvorim intervaly a budu urcovat znamenko vyrazu v absolutni hodnote (rekla bych, ze toto dela nejvetsi problem - jednoduse si predstav nejake cislo z "povoleneho intervalu" a dosad si ho do zapisu s absolutni hodnotou, pokud v absolutni hodnote, vychazi +, tak se znamenko nemeni, jinak zmena na -) Tak to postupne provedu jak pro absolutni hodnotu uvnitr zavorky, tak i pro "velkou" absolutni hodnotu:
(-oo, -1> (-1, 5> (5, +oo)
|3-|2-x|| -(3-2+x) +(3-2+x) +(3+2-x)
Budu resit 3 nerovnice - pro kazdy interval samostatne:
I1
-3+2-x<=2x na intervalu (-oo, -1>
-3x<=1
x>=-1/3 jelikoz reseni nerovnice a interval, na kterem resim, nemaji zadny prunik, tak na 1. intervalu resenim je prazdna mnozina.
I2.
3-2+x<=2x na intervalu (-1, 5>
-x<=-1
x>=1 resenim nerovnice je interval <1, +oo), hledame prunik s intervalem (-1, 5>, resenim nerovnice na tomto intervalu jsou x nalezici <1, 5>.
I3.
3+2-x<=2x
-3x<=-5
x>=5/3 resenim nerovnice je interval <5/3, +oo}, hledame prunik s intervalem (5, +oo), resenim nerovnice na tomto intervalu jsou x nalezici (5, +oo).
Po sjednoceni reseni pro I1, I2, I3 dostaneme, ze x nalezi <1, +oo)
Abych rekla pravdu, tak ja osobne bych resila jedine graficky, ale nejsem si jista, zda by to bylo akceptovano.
Nerovnice v prikladu 3 je jednodussi. A vidim, ze rovnice 1 uz je take vyresena (dekuji kolegovi :-)
Hodne zdaru, ozvi se, zda to slo :-)
Offline
#8 10. 01. 2008 16:25
Re: Lineární rovnice s absolutní hodnotou-slozite
princip je stejny jako se zavorkama, zacnes u tech vnitrnich....
takze v tomhle pripade nejdrive musis odstarnit nejvnitrnejsi AH.
v priklade c 1 je to X+1 ...
Ted musis zjistit nulovy bod
(to je bod, ve kterem absolutni hodnota nabyva 0 a je to předěl mezi tím kdy je kladna a kdy záporná)
Nulový bod zjistis nasledovne: x+1=0 tj x=-1
takze nulovy bod je -1
ten ti rozdeli na dva interavly: -nekonecno až -1 ------ a -1 až nekonečno
když dosadis jakekoli cislo z prvniho intervalu, cislo v AH vyjde zaporne, kdyz z druheho tak kladne...
pokud vnitrek Ah je kladny např /5+7/ tak muzes AH vynechat a prepsat jako 5+7
pokud je zaporny např. /5-7/ tak ji muzes vynechat v tom pripade ze ji celou vynasobis -1 neboli zmenis znamenka takze -5+7
v tvem pripade to tedy jednou prepises a vyresis s x+1 a jednou s -x-1
jako vysledek ti vyjdou rovnice, ve kterych uz bude jen jena AH a cely postup zopakujes...
Zadani tedy rozepises na 2 rovnice, a ty dale na dalsi 2...
snad sem ti pomohl...
Offline
#10 10. 01. 2008 16:55
Re: Lineární rovnice s absolutní hodnotou-slozite
tady je muj postup z prvniho prikladu takto nas to nejak ucily ve skole ale nevyslo me to :( jelikoz me vysli stejna cisla ale u jinych intervalu to same me vyslo te uz i u toho 2 prikladu dam sem svuj postup a reknete mi pls kde mam chybu diky :
prvni priklad :
druhy priklad:
nevim kde delam chybu :( snad na to nekdo prijde
Offline
#12 10. 01. 2008 17:35
Re: Lineární rovnice s absolutní hodnotou-slozite
sklibor napsal(a):
dopracoval jsem se k vysledku 4 prikladu a vyslel my takovyhle vysledek : <1,+nekonecno) a <-5,+nekonecno)
je to dobry vysledek ????
ve 4tem prizpevku mas ten priklad spocitany, co se na to treba mrknout ?
a nezda se ti trosku divny interval od 1 do nekonecna a ode -5ti do nekonecna? ten by se prece sjednotil do -5 az nekonecno...
Offline
#14 25. 02. 2010 20:51
- januska111
- Příspěvky: 42
- Reputace: 0
Re: Lineární rovnice s absolutní hodnotou-slozite
pekný den potřebovala bych pomoct s příkladem -1+x=|5x+1| potřebovala bych ho vypočítat početně i graficky a moc nevimjak na to... moc dekuji za pomoc :-)
Offline
#15 25. 02. 2010 21:27
Re: Lineární rovnice s absolutní hodnotou-slozite
↑ januska111:
rozděl příklad na dva problémy pro x>=-1/5 v x<-1/5
a) pro x>=-1/5 ti tam vyjde -1+x=5x+1 /- (x+1)
4x=-2 /2
x=-1/2 avšak pozor tenhle kořen nesplnuje podmínku x>=-1/5
b) pro x<-1/5
-1+x=1-5x /+5x+1
6x=2
x=1/3
což taky nesplnuje podmínku x<-1/5
tudíž bych řekl že nemá řešení a graficky mi taky žándý nevyšlo
Offline
#16 25. 02. 2010 22:06
- januska111
- Příspěvky: 42
- Reputace: 0
Re: Lineární rovnice s absolutní hodnotou-slozite
dik za pomoc :-)
Offline
#17 25. 02. 2010 22:10
- januska111
- Příspěvky: 42
- Reputace: 0
Re: Lineární rovnice s absolutní hodnotou-slozite
ještě bych se chtela zeptat na priklad 2|x|=x+3 taky početně a graficky děkuji :-)
Offline
#18 25. 02. 2010 22:47
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Lineární rovnice s absolutní hodnotou-slozite
↑ januska111:
Zdravím,
zakladej si prosím nové téma pro své dotazy. Děkuji.
Grafické řešení,
početně:
nulový bod pro |x| je 0,
proto na intervalu od -oo do 0 řešiš rovnici 2(-x)=x+3,
na intervalu od 0 do +oo řešiš rovnici 2x=x+3
Ať se vede.
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » Lineární rovnice s absolutní hodnotou-slozite (TOTO TÉMA JE VYŘEŠENÉ)