Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 23. 02. 2008 18:53
Rozdíl vzdáleností
Tak s tímto nevím.
Najděte na ose y bod P tak, aby měl největší rozdíl vzdáleností od bodů
A = [-3; 2] a B = [2; 5]
Podle zdroje příkladu by neměl být příliš složitý. Proto si myslím, že jsem se dostal do slepé uličky. Došel jsem totiž (po derivování) k rovnici, která byla na celý řádek.
V Mathcadu jsem si vykreslil graf závislosti rozdílu vzdáleností na souřadnici y bodu P. Maximum tam bylo okolo y = -19. Ještě to nějak vypočítat.
Offline
#5 24. 02. 2008 13:27 — Editoval jarrro (16. 12. 2013 12:54)
Re: Rozdíl vzdáleností
[mathjax]P=\left[0, y\right]\\\text{rozdiel vzdialenosti}=\sqrt{\left(-3-0\right)^2+\left(2-y\right)^2}-\sqrt{\left(2-0\right)^2+\left(5-y\right)^2}\\ f{\left(x\right)}=\sqrt{\left(-3-0\right)^2+\left(2-x\right)^2}-\sqrt{\left(2-0\right)^2+\left(5-x\right)^2}=\sqrt{x^2-4x+13}-\sqrt{x^2-10x+29}\\f^{\prime}{\left(x\right)}=\frac{x-2}{\sqrt{x^2-4x+13}}-\frac{x-5}{\sqrt{x^2-10x+29}}\\ f^{\prime}{\left(x\right)}=0\Leftrightarrow \frac{x-2}{\sqrt{x^2-4x+13}}=\frac{x-5}{\sqrt{x^2-10x+29}}\\ \left(x-2\right)\sqrt{x^2-10x+29}=\left(x-5\right)\sqrt{x^2-4x+13}\\ \left(x^2-4x+4\right)\left(x^2-10x+29\right)=\left(x^2-10x+25\right)\left(x^2-4x+13\right)\\ x^4-10x^3+29x^2-4x^3+40x^2-116x+4x^2-40x+116=x^4-4x^3+13x^2-10x^3+40x^2-130x+25x^2-100x+325\\ 29x^2-116x+4x^2-40x+116=13x^2-130x+25x^2-100x+325\\ 33x^2-156x+116=38x^2-230x+325\\ 5x^2-74x+209=0\\ x_1=11\\ x_2=3.8\\ x_2 \text{ nevyhovuje}[/mathjax]
MATH IS THE BEST!!!
Offline
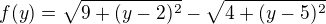 , kde y je y-ova vzdalenost hledaneho bodu a pak hledas extrem teto fce, respektive tedy maximum
, kde y je y-ova vzdalenost hledaneho bodu a pak hledas extrem teto fce, respektive tedy maximum