Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z diskrétní matematiky
- » Pomoc s grafmi (TOTO TÉMA JE VYŘEŠENÉ)
#1 09. 02. 2010 09:33
Pomoc s grafmi
Ahoj, potrebovala by som pomocť s dvoma príkladmi na grafy.
1) "Mějme dán rovinný graf G, jehož všechny stupně jsou alespoň 5. Dokažte, že nutně musí mít alespoň 12 vrcholů."
2) "Mějme dán souvislý graf G. Dokažte, že pro každou hranu e /z/ E(G) existuje kostra K grafu G, která hranu e obsahuje."
Offline
- (téma jako vyřešené označil(a) prakovce)
#2 09. 02. 2010 10:08 — Editoval Wotton (09. 02. 2010 10:09)
Re: Pomoc s grafmi
Zdravím,
1) Víme že v roviném grafu platí nerovnost 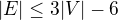 Protože všechny vrcholy jsou alespon stupně 5, tak musí platit nerovnost
Protože všechny vrcholy jsou alespon stupně 5, tak musí platit nerovnost  To když spojíme tak máme
To když spojíme tak máme  . Zbytek už zvládneš sama.
. Zbytek už zvládneš sama.
2) Zvolme si hranu (u;v) v G. Mějme F kostru grafu G takovou že neobsahuje hranu (u;v). Nyní musí vést z u do v cesta v F. Když na této cestě odstraníme libovolnou hranu, tak se nám kostra F rozpadne na 2 komponenty. Když k těmto komponentám přídáme hranu (u;v), tak nám vznikne graf F' který je kostrou grafu G.
Dva jsou tisíckrát jeden.
Offline
#3 09. 02. 2010 21:04
Re: Pomoc s grafmi
↑ Wotton:U 2) navrhuji alternativu. Zvolíme libovolnou kostru F. Pokud hranu e obsahuje, jsme hotovi. Pokud ji F neobsahuje, tak F s přidanou hranou e obsahuje právě jeden cyklus/kružnici (cesta mezi u a v spolu s hranou e - navic je to věta, která se objevuje ve většině učebnic). Z toho cyklu vynecháme libovolnou hranu různou od e a dostaneme souvislý acyklický faktor, čili kostru.
Offline
#4 09. 02. 2010 21:07
Re: Pomoc s grafmi
↑ prakovce:Mimochodem, to tvrzení nejde zesílit. Vskutku existuje 5-pravidelný graf na 12 vrcholech. Jaký?
Offline
#5 12. 02. 2010 13:19
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z diskrétní matematiky
- » Pomoc s grafmi (TOTO TÉMA JE VYŘEŠENÉ)
