Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Důkaz, součet kombinačních čísel (TOTO TÉMA JE VYŘEŠENÉ)
#1 08. 03. 2010 16:08
- teolog


- Místo: Praha
- Příspěvky: 3497
- Škola: MFF + PřF UK
- Pozice: Gymnázium Přírodní škola - učitel (M, Z)
- Reputace: 167
Důkaz, součet kombinačních čísel
Zdravím všechny. Chtěl bych poprosit o pomoc s následujícím příkladem:
Dokažte, že pro všechna přirozená čísla n a k splňující  platí:
platí:
Offline
- (téma jako vyřešené označil(a) stepan.machacek)
#3 08. 03. 2010 21:46
- teolog


- Místo: Praha
- Příspěvky: 3497
- Škola: MFF + PřF UK
- Pozice: Gymnázium Přírodní škola - učitel (M, Z)
- Reputace: 167
Re: Důkaz, součet kombinačních čísel
↑ musixx:
Díky za nakopnutí, ale pořád nějak tápu.
Můj pokus:
1.Dokázat, že to platí pro k=1 a n=1. Není potřeba rozepisovat.
2.Dokázat, že to platí pro k+1 a n+1:
po úpravě levé strany
pak jsem zkoušel toto:
ale dál už moc nevím. Navíc jsem si teď při přepisování do TeXu uvědomil, že při důkazu požívám to, co dokazuji. Což nelze.
Můžete mi ještě trochu napovědět, jak dál?
Offline
#4 08. 03. 2010 23:01
Re: Důkaz, součet kombinačních čísel
Indukciu urobíme pre 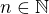 . Číslo
. Číslo  je pevne zvolené ľubovoľné. Na to sa indukcia nevzťahuje. Množina prirodzených čísel je nekonečná a nikdy nevieme, či niečo nevyskočí. S číslom k budeme zaobchádzať všeobecne. Predpokladáme teda platnosť
je pevne zvolené ľubovoľné. Na to sa indukcia nevzťahuje. Množina prirodzených čísel je nekonečná a nikdy nevieme, či niečo nevyskočí. S číslom k budeme zaobchádzať všeobecne. Predpokladáme teda platnosť 
Ukazujeme pre n+1 a pevne zvolené k:
Čo je opäť identita známa napríklad z Pascalovho trojuholníka. Korektne by sa to malo robiť "pospiatky" aby šlo o dôkaz. Mne sa to však zdá zbytočné prepisovanie, aj tak každý to urobí najprv takto.
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#5 09. 03. 2010 00:35
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Důkaz, součet kombinačních čísel
Když to zapíšeš takhle, tak není žádný problém s tím, že bys to správně měl dělat od konce.
Já bych to ale stejně asi dělal bez indukce, mnohonásobným použitím vzorce, který navrhoval musixx.
Offline
#6 09. 03. 2010 11:10
- teolog


- Místo: Praha
- Příspěvky: 3497
- Škola: MFF + PřF UK
- Pozice: Gymnázium Přírodní škola - učitel (M, Z)
- Reputace: 167
Re: Důkaz, součet kombinačních čísel
Všem díky za snahu. Jen bych se ještě optal. Lukaszh ve svém postupu na začátku předpokládá platnost dokazovaného vzorce a během postupu tento vzorec použije. Ale nejsem si jistý, jestli může v důkazu něčeho to něco použít.
Jinak v té indukci jsem měl trochu zmatek, zda dokazuji jen pro n+1 nebo i k+1, takze lukaszh mi to ujasnil.
A také díky BrozkoviP, jeho postup mi přijde elegantní.
Offline
#7 10. 03. 2010 16:51
Re: Důkaz, součet kombinačních čísel
o tom je indukcia,že predpokladáme pre nejaké n že dokazované platí a snažíme sa z toho dostať,že to platí aj pre prirodzené číslo o jedna väčšie potom z platnosti pre n=1 vyplýva platnosť pre n=2 stade pre n=3 atď
MATH IS THE BEST!!!
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Důkaz, součet kombinačních čísel (TOTO TÉMA JE VYŘEŠENÉ)
 .
.