Matematické Fórum

Petuhik · 11. 03. 2010 17:29

ahoj, chtěla bych se zeptat, jak mám postupovat, abych určila transformační rovnice kolmé projekce do roviny a kolmý průmět přímky AD. Ten průmět mám, ale na ten první bod nemůu přijít:-(. Děkuji mnohokrát za pomoc.

ρ = BEG B [6,0,0]; E[0,0,6]; G[6,3,6]

obecná rovnice roviny: x-2y+z-6=0

Rumburak

Mějme obecný bod $X = [x,\,y,\,z]$ a hledejme jeho průmět $f(X) = [u,\,v,\,w]$ do roviny BEG.

Normálový prostor roviny BEG je určen vektorem $\vec n\,:=(1,\, -2, \,1)$ (sestaveným z koeficientů u x,y,z v té rovnici x-2y+z-6=0 ).
Bod 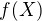$f(X)$ má dvě vlastnosti :

1. Leží v rovině BEG - jeho souřadnice tedy splňují rovnici této roviny, takže platí

(1) $u-2v+w-6=0$ .

2. Vektor $f(X)-X$ je kolmý k rovině BEG, leží tedy v jejím normálovém prostoru, takže existuje r.č. $\lambda$ takové, že $f(X)-X = \lambda \vec n$ .
Odtud vyjádříme $f(X) = X + \lambda \vec n = [x+\lambda, \,y-2\lambda, \,z + \lambda]$ , tedy

(2) $u = x+\lambda, \,v =y-2\lambda, \,w=z + \lambda$ .

Zbývá dopočítat číslo $\lambda$ . K tomu dosadíme (2) do (1) , tím dostaneme rovnici $x+\lambda-2(y-2\lambda)+z +\lambda-6=0$ pro neznámou $\lambda$
(v závislosti na souřadnicích x, y, z zvoleného bodu X) .
Vypočítané $\lambda(x,\,y,\,z)$ pak dosadíme do rovnic (2) a tento výsledek ještě vhodně upravíme, případně vyjádříme v maticovém tvaru.

Matematické Fórum

#1 11. 03. 2010 17:29

projekce

#2 12. 03. 2010 09:55 — Editoval Rumburak (12. 03. 2010 10:04)

Re: projekce

Zápatí