Matematické Fórum

princess21 · 12. 03. 2010 19:23

no zase problem s komplexnymi cislami. ak mam jednoduchy priklad typu z=5+3i tak mi to ide, ale v testoch som narazila na takyto typ: z= (6-2i) / (8+4i)

a ten mi vobec ale vobec nevychadza. skusala som to pocitat tak ze som vypocitala podiel a tak z toho urobit gon. tvar, lenze to je asi blbost lebo mi to nevychadza ani v jednom z 5tich typov, mozte ma trosku nakopnut? :)

N3st4 · 12. 03. 2010 19:30

Cau. A co s tym presne chces urobit ? Vypocitat podiel ?

princess21 · 12. 03. 2010 19:32

goiometricky tvar

N3st4 · 12. 03. 2010 19:37

Urcite to nejde s tym podielom vypocitat ... ? A ak sa ti zda, ze nie tak to pocitaj v zlomku ... resp. ak mas vysledok, tak ho napis a poviem ti, ci som sa dopracoval k rovnakemu.

hradecek

↑ princess21:
Skús napísať postup ako si to riešila.
Po vydelení by si mala dostať 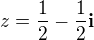$z = \frac{1}{2}-\frac{1}{2}\mathbf i$
absolútna hodnota 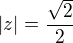$|z|=\frac{\sqrt{2}}{2}$
$sin \varphi=\frac{\sqrt{2}}{2}=45^\circ$
$cos \varphi=\frac{\sqrt{2}}{2}=45^\circ$
$G.T.$
$z=\frac{\sqrt{2}}{2}(cos 45^\circ+i.sin 45^\circ)$

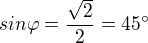
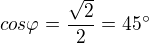
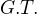
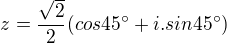
Stačí tak ?

N3st4 · 12. 03. 2010 20:12

°) ja som myslel, ze chce aby bola k tomu navedena a nie to rovno vypocitat :D, ale inak je to dobre ;) Mam to rovnako.

hradecek · 12. 03. 2010 20:21

↑ N3st4:Ja som napísal iba výsledky, ktorých by sa mala držať. Pre výpočet musíš spraviť o niečo málo viac ;-).

N3st4 · 12. 03. 2010 20:25

Tak tak. Mimochodom odporucam vrele webstranku priklady.eu ...
Je tam skoro cela stredoskolska matematika, vratane C.

princess21 · 12. 03. 2010 21:24

jeej chalani dakujem, nasla som si chybu, ja som si poplietla vzorec na ten podiel, to preto mi nevychadzalo 0:) N3st4 diky za stranku, snad pomoze v niecom :)

Matematické Fórum

#1 12. 03. 2010 19:23

gon. tvar koplexneho cisla

#2 12. 03. 2010 19:30

Re: gon. tvar koplexneho cisla

#3 12. 03. 2010 19:32

Re: gon. tvar koplexneho cisla

#4 12. 03. 2010 19:37

Re: gon. tvar koplexneho cisla

#5 12. 03. 2010 19:58 — Editoval hradecek (12. 03. 2010 20:08)

Re: gon. tvar koplexneho cisla

#6 12. 03. 2010 20:12

Re: gon. tvar koplexneho cisla

#7 12. 03. 2010 20:21

Re: gon. tvar koplexneho cisla

#8 12. 03. 2010 20:25

Re: gon. tvar koplexneho cisla

#9 12. 03. 2010 21:24

Re: gon. tvar koplexneho cisla

Zápatí