Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Diskrétní matematika - Dokažte indukcí (TOTO TÉMA JE VYŘEŠENÉ)
#1 13. 03. 2010 12:14
Diskrétní matematika - Dokažte indukcí
Dokažte indukcí, že 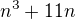 je číslo dělitelné šesti pro všechna přirozená
je číslo dělitelné šesti pro všechna přirozená  .
.
Tedy udelal jsem nasledne: 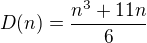 .
.
Zakladni krok: n = 1 - to delitelne je...
Indukcni krok: misto n jsem dosadil n + 1 a dal si uz nejak nevim rady.
Za jakoukoliv pomoc dekuji moc. :)
********
********
* O = O *
_
Offline
- (téma jako vyřešené označil(a) halogan)
#7 13. 03. 2010 12:58
Re: Diskrétní matematika - Dokažte indukcí
↑ halogan: je to vzdy sude cislo, a ro po vynasobeni 3 v sebe obsahuje 3*2 cize 6!!!!!!!!!!!
a je to...
Offline
#10 13. 03. 2010 16:35
Re: Diskrétní matematika - Dokažte indukcí
↑ Frantik88:Jen mimochodem: kdyby to nemělo být dokázáno indukcí, tak můžeme postupovat třeba takto: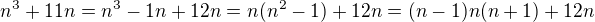
Další argumentace je podobná, neboť výsledný výraz je jistě dělitelný 2 i 3 a proto 6.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Diskrétní matematika - Dokažte indukcí (TOTO TÉMA JE VYŘEŠENÉ)


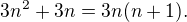
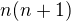 ?
?