Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 18. 03. 2010 09:22 — Editoval Marian (18. 03. 2010 09:23)
Řešení rovnice
Nechť je dána rovnice 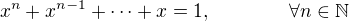
s neznámou ![kopírovat do textarea $x\in [0,1]$](/mathtex/78/78bb3465294c0a7bd59c6a1cdea9a087.gif) . Dokažte, že
. Dokažte, že
(1) existuje řešení této rovnice na uvedeném intervalu pro libovolné n,
(2) řešení závisí na volbě čísla n - označte ho jako  ,
,
(3) najděte 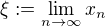 .
.
Úloha se dá řešit snadno a bod (3) lze "řešit" uhodnutím, ale berte to jako cvičení s požadavkem na maximálně transparentní řešení a korektní důkazy všech tvrzení (1)-(3) a všech pomocných tvrzení. Rozsah látky potřebné k řešení není (nemusí být) větší než úvodní kurs analýzy na VŠ.
Offline
- (téma jako vyřešené označil(a) byk7)
#2 18. 03. 2010 11:31 — Editoval Pavel (18. 03. 2010 12:25)
Re: Řešení rovnice
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#3 18. 03. 2010 14:03 — Editoval Rumburak (18. 03. 2010 16:07)
Re: Řešení rovnice
Snažil jsem se postupovat hodně podrobně, čímž jsem přišel o "modrou stuhu". :-)
Místo do Algebry bych to zařadil do Analýzy.
Offline
#4 18. 03. 2010 20:59
- check_drummer

- Příspěvky: 4952
- Reputace: 106
Re: Řešení rovnice
V podstatě se jedná o rovnice: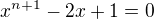
"Máte úhel beta." "No to nemám."
Offline
#5 19. 03. 2010 14:15 — Editoval musixx (19. 03. 2010 14:35)
Re: Řešení rovnice
S tím zařazením do analýzy...
Offline
#7 20. 03. 2010 14:12
Re: Řešení rovnice
↑ Pavel:↑ Rumburak:↑ musixx:
Výborně. Mé řešení se pouze mále liší od Pavlova a Rumburakova. Přístup od musixx je skutečně algebraický.
Zároveň souhlasím s tím, že to mohlo být zařazeno do analýzy, ale chtěl jsem trochu prohřát i tuto sekci. Navíc je vidět, že lze řešit problém i algebraickým aparátem.
Offline

 je na intervalu
je na intervalu ![kopírovat do textarea $[0,1]$](/mathtex/52/520897da7413e2014a7783a154b21dba.gif) spojitá a platí
spojitá a platí  a
a  . Tzn. existuje bod
. Tzn. existuje bod ![kopírovat do textarea $t\in[0,1]$](/mathtex/78/7855e6e15435ece52cfb477247d43585.gif) , pro který platí
, pro který platí 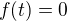 .
.  , pak by obě rovnice
, pak by obě rovnice  a
a  měly stejná řešení, což nemají.
měly stejná řešení, což nemají. bude kořenem rovnice
bude kořenem rovnice 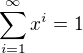 . Protože stačí uvažovat
. Protože stačí uvažovat 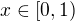 (pro
(pro 
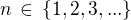 .
.![kopírovat do textarea $x\,\in\,[0,\,1]$](/mathtex/92/92118898953abddeab59154d5c721278.gif) definujme
definujme 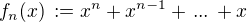 .
. 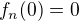 ,
, 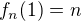 , pří čemž
, pří čemž 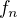 je funkce, která je v intervalu
je funkce, která je v intervalu ![kopírovat do textarea $[0,\,1]$](/mathtex/f5/f50f9da34079d25c0810ee32df2d07cc.gif) na interval
na interval ![kopírovat do textarea $[0,\,n]$](/mathtex/c2/c2a4beb2667226b346939c3558cb1b3c.gif) , zároveň
, zároveň ![kopírovat do textarea $1\,\in\,[0,\,n]$](/mathtex/4a/4a721d08b1ec29c61fe6ae71d59f3952.gif) , odtud existence a jednoznačnost řešení
, odtud existence a jednoznačnost řešení 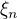
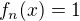 na intervalu
na intervalu 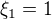 , v ostatních případech
, v ostatních případech  .
.![kopírovat do textarea $x\,\in\,(0,\,1]$](/mathtex/6f/6f5e6808c04ac0f46571a23897cefa4d.gif) je poslouopnost
je poslouopnost 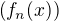 rostoucí, takže má-li
rostoucí, takže má-li  být posloupnost, která je
být posloupnost, která je být klesající - nechť
být klesající - nechť 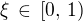 je její infimum (a zároveň limita). Jistě tedy existují čísla
je její infimum (a zároveň limita). Jistě tedy existují čísla  ,
,  taková, že
taková, že pro libovolná
pro libovolná 
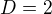 ,
, 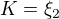 ) , odtud
) , odtud  pro libovolná
pro libovolná 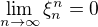 .
. je
je  , takže
, takže 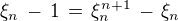 ,
,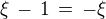 ,
, 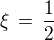 .
.
 (tzv. formální derivace zavedená v algebře)
(tzv. formální derivace zavedená v algebře)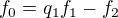 dává snadno
dává snadno 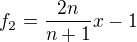
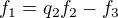 dává již trošku s počítáním
dává již trošku s počítáním  (
(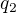 jde celkem snadno najít s podmínkou, že
jde celkem snadno najít s podmínkou, že 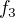 už musí být konstanta;
už musí být konstanta; , kde aby se to hezky odčítalo a celkem to až na konstantu dalo
, kde aby se to hezky odčítalo a celkem to až na konstantu dalo 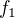 , tak v A, B, atd. se budou postupně navyšovat mocniny u toho koeficientu, jako je u
, tak v A, B, atd. se budou postupně navyšovat mocniny u toho koeficientu, jako je u 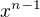 -- pak stačí jen výsledné
-- pak stačí jen výsledné 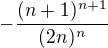 (tj. až na znaménko absolutní člen ve
(tj. až na znaménko absolutní člen ve  ,
,  ,
,  ,
,  dává
dává 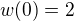 .
. ,
,  ,
,  ,
,  dává
dává  .
.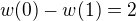 kořeny, ale ten
kořeny, ale ten 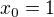 jsme si schválně přidali. Proto zbývá jediný kořen na
jsme si schválně přidali. Proto zbývá jediný kořen na 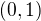 , což jsme potřebovali ukázat.
, což jsme potřebovali ukázat.