Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#4 29. 03. 2010 20:41
Re: magnet.p
↑ sanr:
Bude to jinak. Opět se podívej na studijní text, na který odkazuje Zdenek1. Konkrétně na vztah (24), který platí pro vodič konečné délky. U magnetické intenzity platí princip superpozice, takže můžeme spočítat magnetické pole zvlášť pro obě polopřímky vodiče rozdělené v bodě jejich zalomení a pak sečíst. Podle vztahu (24) v uvedeném studijním textu je hodnota magnetické intenzity úsečky dána vztahem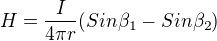
Pro případ polopřímkového vodiče (kraji vodiče, který je v nekonečnu, uvažujeme že svírá úhel 90 stupňů s průvodičem) tedy bude vypadat vztah v našem případě takto
Úhel mimochodem beru v radiánech. Úvahu o tom, jak jsem na ten úhel přišel rozepisovat nebudu. Stačí si pořádně přečíst, co ty úhly beta ve vztahu (24) znamenají a trochu se nad tím geometricky zamyslet.
Tím tedy máme spočítanou hodnotu pro jednu polopřímku. Pro druhou to musí vyjít stejně, protože je to symetrická situace. Výsledná H tedy bude mít hodnotu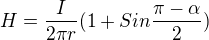
Ale také pozor na jednu věc. r není rovno a. r je kolmá vzdálenost k vodiči, kdežto a je vzdálenost od zalomení vodiče, čili platí
Takže výsledek bude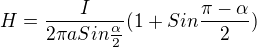
Chceme-limagnetickou indukci, stačí přenásobit permeabilitou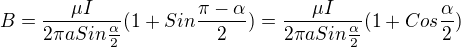
1 + 1 = 1 + 1
... a nebo taky ne
Offline
#6 30. 03. 2010 01:43 — Editoval medvidek (30. 03. 2010 02:34)
Re: magnet.p
↑ sanr:
Úloha 4:
Vzorec pro kruhovou proudovou smyčku je "učebnicový":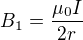
Vzorec pro čtvercovou smyčku lze odvodit například tak, že navážeme na výpočet pole pro přímý úsek vodiče uvedený zde http://forum.matweb.cz/viewtopic.php?id=15879  ,
,
kde  je kolmá vzdálenost od přímého úseku vodiče a
je kolmá vzdálenost od přímého úseku vodiče a  je délka úseku vodiče (viz obrázek v daném tématu).
je délka úseku vodiče (viz obrázek v daném tématu).
Rozdělíme-li čtvercovou smyčku o délce strany  na 8 stejných přímých úseků o délce
na 8 stejných přímých úseků o délce 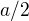 , můžeme použít vzorec pro
, můžeme použít vzorec pro  na každý z těchto úseků, přičemž
na každý z těchto úseků, přičemž 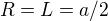 . Po dosazení za R a L a vynásobení 8 dostaneme pro čtvercovou smyčku o straně
. Po dosazení za R a L a vynásobení 8 dostaneme pro čtvercovou smyčku o straně  následující vztah
následující vztah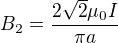 .
.
Nyní stačí správně dosadit rozměry smyček do vzorců pro 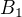 a
a  a výsledky porovnat.
a výsledky porovnat.
Magnetická indukce bude nejmenší ve velké kruhové smyčce a největší v malé kruhové smyčce.
Poměr velikostí mag. indukce od nejmenší po největší je  .
.
EDIT: úprava odkazu
Offline
#7 30. 03. 2010 02:07 — Editoval medvidek (30. 03. 2010 02:15)
Re: magnet.p
↑ sanr:
Úloha 5:
U cívky by bylo na místě upřesnit, kde v ose cívky má být pole vypočteno (uprostřed, na koncích nebo někde jinde). Předpokládejme ale, že nás zajímá pouze střed cívky, protože tam je mag. indukce největší.
Pro tak úzkou a dlouhou cívku resp. toroid by měly být výsledky téměř stejné. Vyšlo mi
5a) toroid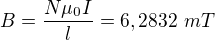 , kde
, kde 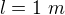 je obvod v ose toroidu (délka zkroucené cívky).
je obvod v ose toroidu (délka zkroucené cívky).
5b) solenoid
Offline
#8 30. 03. 2010 17:19
Re: magnet.p
Napadlo mě ještě k úloze 4.
Úloha lze řešit tím, že mám-li vodič tvořen rovinnou křivkou, pak magnetickou indukci v počátku souřadnic (požívám polární souřadnice) je dán vztahem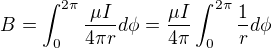
Integraci provádíme podél úhlové souřadnice, přes kterou "sčítáme" převrácenou hodnotu vzdálenosti vodiče od bodu, kde magnetickou indukci počítáme. Z tohoto nutně plyne následující. Mám-li první vodič uzavřenou křivku a druhý, který je také uzavřenou křivkou a je "uvnitř" prvního vodiče (je jím jakoby omezen), pak ten první (větší) bude určitě dávat do bodu, který je uvnitř obou vodičů menší magnetickou indukci. To proto, že pro všechna  je hodnota 1/r u většího vodiče menší. Musí tedy být menší i po integraci, vzhledem k tomu, že u obou vodičů integrujeme přes stejný interval. Je to poměrně dobře představitelné, snad jsem to popsal srozumitelně.
je hodnota 1/r u většího vodiče menší. Musí tedy být menší i po integraci, vzhledem k tomu, že u obou vodičů integrujeme přes stejný interval. Je to poměrně dobře představitelné, snad jsem to popsal srozumitelně.
Odtud tedy ihned plyne, který vodič bude mít vyšší a který nižší magnetickou indukci uprostřed závitu. Tato myšlenka lze použít na zcela libovolné uzavřené rovinné smyčky. Nemusí to být žádný symetrický případ typu kruh, čtverec a není třeba si dohledávat pro tyto tvary konkrétní vzorečky a magnetickou indukci přímo počítat.
1 + 1 = 1 + 1
... a nebo taky ne
Offline
#10 10. 04. 2010 21:17 — Editoval sanr (10. 04. 2010 21:38)
Re: magnet.p
mohl by mi někdo pomoct PLS, tyto poslední příklady mi nějak nejdou , ta 5. otačivý moment působí na kruhový závit - tam by měla být potenciální energie největší v tom případě a- jenže je to 90° - cos 90°=0 a když je Ep=- I pi r^2 (mí)o H cos(fí), tak mi vychází že je naopak případ c největší Ep ,nějak v tom plavu, dik za rady
toto je dalsi taky maras
Offline