Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Princip inkluze a exkluze v sumě kombinačních čísel
#1 22. 03. 2010 00:07
Princip inkluze a exkluze v sumě kombinačních čísel
Totálně jsem se zasekl u této úlohy:
Pomocí vhodné kombinatorické interpretace a použitím principu inkluze a exkluze spočítejte nasledující sumu pro n,m,j přirozené takové, že n ≤ j ≤ (m + n), t.j. vyjádřete tuto sumu jako nějaký výraz, který už bude bez sumy:
Ať na to koukám, jak chci, PIE tam nikde nevidím. Nevidíte ho tam někde vy?
Offline
#2 22. 03. 2010 11:42
Re: Princip inkluze a exkluze v sumě kombinačních čísel
Á, tato úložka mě ze všech v diskrétce bavila nejvíce. Dám jen tipy: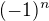 poměrně jasně odkazuje na princip inkluze a exkluze - vždyť i v jeho vyjádření vzorcem se to nachází.
poměrně jasně odkazuje na princip inkluze a exkluze - vždyť i v jeho vyjádření vzorcem se to nachází.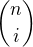 je počet i-prvkových podmnožin n-prvkové množiny. Vzhledem k tomu, že se v PIE sčítá přes všechny možné počty množin v průniku, chtělo by to najít takový systém
je počet i-prvkových podmnožin n-prvkové množiny. Vzhledem k tomu, že se v PIE sčítá přes všechny možné počty množin v průniku, chtělo by to najít takový systém  množin, ve kterém má průnik každých
množin, ve kterém má průnik každých  množin stejnou velikost pro
množin stejnou velikost pro  . A nejlépe by bylo, kdyby velikost toho průniku pak byla
. A nejlépe by bylo, kdyby velikost toho průniku pak byla  .
.
Offline
#3 22. 03. 2010 12:17
Re: Princip inkluze a exkluze v sumě kombinačních čísel
přidám svou trošku do mlýna: mám  jablek a
jablek a  hrušek.
hrušek. ... vyberu si
... vyberu si  hrušek a k nim
hrušek a k nim 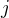 kusů libovolného ovoce
kusů libovolného ovoce ... odečtu případy, kdy si vyberu
... odečtu případy, kdy si vyberu  hrušku a doplním do
hrušku a doplním do 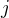 kusů libovolně
kusů libovolně ... přičtu zpátky případy, kdy si vyberu
... přičtu zpátky případy, kdy si vyberu  hrušky a zbytek libovolně
hrušky a zbytek libovolně
...
teď se zamyslím, co takovýmhle způsobem můžu pomocí PIE spočítat;)
Offline
#4 24. 03. 2010 21:54
Re: Princip inkluze a exkluze v sumě kombinačních čísel
↑ Stýv:
Právě to je to, co mi uniká. Zkoušel jsem si to nakreslit a poupravit zadanou sumu, ale vycházejí mi stále prazvláštní součiny kombinačních čísel. Wolfram Alpha – http://www.wolframalpha.com/input/?i=su … j%3D0+to+n – dává výsledek plný funkcí, se kterými jsem se doposud nesetkal. Dospěl jsem akorát k tomu, že v součinu uvnitř sumy je kromě n-tého kombinačního čísla i součin prvků na "diagonále" v Pascalově trojúhelníku. Pokoušel jsem se to vyjádřit jako součin prvků, ale stále mi to nevychází.
V čem dělám chybu? Nešlo by ten vnitřek sumy vyjádřit nějak jinak, aby se s tím lépe počítalo?
Offline
#5 24. 03. 2010 23:06
Re: Princip inkluze a exkluze v sumě kombinačních čísel
není třeba nic počítat, stačí použít tu úvahu... napíšu jí ještě jinak:
1. spočítám si všechny možný výběry
2. odečtu ty, který obsahujou hrušku
3. protože jsem některý odečetl víckrát, tak je zase zpátky přičtu, zase sem jich přičetl moc, tak některý odečtu ... prostě standardní použití PIE
třetí bod jsou víceméně takový korekce, takže se zamysli, co dávají první dva body;)
ps: pokud píšu nějaký nesmysly, tak mě někdo zarazte:)
Offline
#6 04. 11. 2014 23:15
Re: Princip inkluze a exkluze v sumě kombinačních čísel
↑ Stýv:
Dobrý den,
řeším stejnou úlohu. Vzal jsem si jako příklad 2 hrušky (n), 2 jablka (m) a vybírám 3 kusy ovoce (j). Po dosazení do vzorce uvedeného v prvním příspěvku mi vychází počet výběrů 0, přitom má podle mě vyjít 2 (výběr 2 hrušek a 1 jablka nebo 1 hrušky a 2 jablek). Dále nerozumím, co znamenají všechny možné výběry v bodě 1.
Předem děkuji za Vaše názory.
Offline
#7 07. 11. 2014 17:31
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Princip inkluze a exkluze v sumě kombinačních čísel
Zdravím,
vzhledem k sestavě diskutujících přesunu do Pokročilých VŠ.
↑ auditor: já tomu rozumím tak, že kolega Stýv všemi výběry rozumí, že vybere potřebný počet ovoce, bez ohledu na to, co to je za ovoce. Potom to probírá a vyřazuje skladby, co se mu nehodí.
Stýv napsal(a):
ps: pokud píšu nějaký nesmysly, tak mě někdo zarazte:)
Kdo by si to dovolil, kolego Stýve? :-)
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Princip inkluze a exkluze v sumě kombinačních čísel
