Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 23. 03. 2010 19:45
Exponenciálna rovnica
Ahoj mám tu takúto rovnicu a nejak mi stále nechce vyjsť správny výsledok a už som v koncoch.
Pokiaľ by sa dalo tak bez pomoci logaritmovania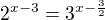
Netrápte sa nad svojimi problémami s matematikou, môžem vás uistiť, že tie moje sú ešte väčšie. ~~Albert Einstein~~
Jak spozná člověk, že není pitomec ? - Moudrý člověk to nepozná nikdy a blbci je to jedno. ~~Jak přicházejí básnici o iluze~~
Někteří lidi se nikdy nezmění. Anebo se rychle změní a pak se zase rychle změní nazpátek. ~~Homer Simpson~~
Offline
- (téma jako vyřešené označil(a) hradecek)
#2 23. 03. 2010 20:42
Re: Exponenciálna rovnica
↑ hradecek: Myslím , že bez logaritmování to nepůjde.
Jedna krát jedna je " tisíckrát " jedna :-)
Offline
#3 23. 03. 2010 21:14
Re: Exponenciálna rovnica
A mohla by si prosím ťa na ukážku ako sa to počíta s logaritmovaním ? , to mi moc nejde.
Netrápte sa nad svojimi problémami s matematikou, môžem vás uistiť, že tie moje sú ešte väčšie. ~~Albert Einstein~~
Jak spozná člověk, že není pitomec ? - Moudrý člověk to nepozná nikdy a blbci je to jedno. ~~Jak přicházejí básnici o iluze~~
Někteří lidi se nikdy nezmění. Anebo se rychle změní a pak se zase rychle změní nazpátek. ~~Homer Simpson~~
Offline
#4 23. 03. 2010 21:21
Re: Exponenciálna rovnica
↑ hradecek: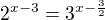 obě strany rovnice zlogaritmujeme. Základ si můžeš vybrat, vyberu dekadický logaritmus
obě strany rovnice zlogaritmujeme. Základ si můžeš vybrat, vyberu dekadický logaritmus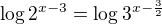



Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#5 23. 03. 2010 21:32
Re: Exponenciálna rovnica
↑ zdenek1:Aha no to ešte celkom chápem. Vďaka.
Netrápte sa nad svojimi problémami s matematikou, môžem vás uistiť, že tie moje sú ešte väčšie. ~~Albert Einstein~~
Jak spozná člověk, že není pitomec ? - Moudrý člověk to nepozná nikdy a blbci je to jedno. ~~Jak přicházejí básnici o iluze~~
Někteří lidi se nikdy nezmění. Anebo se rychle změní a pak se zase rychle změní nazpátek. ~~Homer Simpson~~
Offline
#6 23. 03. 2010 21:44
Re: Exponenciálna rovnica
Jen bych dodal, že to jde bez logaritmování, ale nikoliv bez logaritmu - je totiž  , takže rovnici můžeme upravit na
, takže rovnici můžeme upravit na
a porovnáním exponentů .
.
V podstatě ale jde o tentýž postup, jen jinak zapsaný.
Offline

