Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 25. 03. 2010 16:25
- check_drummer

- Příspěvky: 5447
- Reputace: 106
Re: Libovolny jazyk - dukaz
Co je to  ? L libovolněkrát iterované?
? L libovolněkrát iterované?
"Máte úhel beta." "No to nemám."
Online
#4 25. 03. 2010 20:08
Re: Libovolny jazyk - dukaz
je tohle dukaz?
Pokud mame  tak to muzem odvodit jako L = L, L* = L0 U L1 U L2 U .... tj. L* - L = L =
tak to muzem odvodit jako L = L, L* = L0 U L1 U L2 U .... tj. L* - L = L = 
Dle definice plati L1 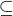 L2 nad abecedou
L2 nad abecedou  : L1
: L1 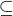 L2 = {xy| x
L2 = {xy| x 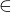 L1, y
L1, y 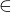 L2}, ztoho plyne ze v nasem pripade pokud mam L
L2}, ztoho plyne ze v nasem pripade pokud mam L 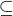 L = {{x| x
L = {{x| x 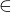 L} je zretezeny jazyk L podmnozinou L.
L} je zretezeny jazyk L podmnozinou L.
Je tohle dukaz?
Offline
 prave, kdyz
prave, kdyz