Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Nekonečný součin (TOTO TÉMA JE VYŘEŠENÉ)
#2 25. 03. 2010 20:13 — Editoval Pavel (26. 03. 2010 14:52)
Re: Nekonečný součin
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#3 26. 03. 2010 14:18
Re: Nekonečný součin
↑ Pavel:
Ano, to je správná technika. Nevidím sice moc pravé strany výpočtů, ale z toho, co vidím, je to patrné. Chtěl bych také upozornit na fakt, že zápis pomocí funkce Gamma(z) je výrazně přehlednější. Ale méně zkušenému čtenáři bude přístupnější Pavlův zápis (uvidí-li pravé strany :-).
Jen mě trochu děsí pojem poslat N do nekonečna. Jinak nemám zvláštních připomínek. Úloha patří do mé osobní dílny nekonečných procesů.
Offline
#4 26. 03. 2010 14:54
Re: Nekonečný součin
↑ Marian:
Díky za připomínku, pravé strany jsem zviditelnil. Z důvodu, který uvádíš, jsem se chtěl právě funkci 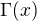 vyhnout.
vyhnout.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#5 15. 05. 2011 15:05
Re: Nekonečný součin
Zdravím, chtěl bych se zeptat, není v některých případech výhodnější převést si součin na součet?
Třeba v tomto případě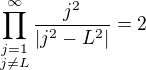
by nám po zlogaritmování "stačilo" dokázat, že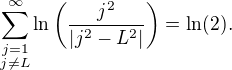
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#6 16. 05. 2011 10:36
Re: Nekonečný součin
↑ byk7:
Je pravdou, že tento přepis někdy pomáhá. Ovšem stále trvá technický problém, jak sečíst obecnou nekonečnou řadu obsahující logaritmy kladných čísel. Pokud bychom chtěli použít teleskopickou metodu, tak bychom si příliš nepomohli přepisem na nekonečnou řadu, protože v takovém případě je možné použít u výpočtu nekonečného součinu (nazvěme to třeba) multiplikativní variantu teleskopické metody (de facto krácení).
Ale nejdůležitější poznámkou zůstává fakt, že někdy tuto teleskopickou metodu nedokážeme aplikovat a není současně možné obdržet nějakou snadnější úvahou výsledek pomocí přepisu na nekonečnou řadu. To je třeba případ nekonečného součinu
Tam bych doporučil použít definici nekonečného součinu (tj. uvážit limitu parciálních součinů) a tu vypočítat. Otázkou pak ale je, jak obecně a zásadně jinak vyjádřit paricální součin. Pokud ale má obecný činitel v nekonečném součinu tvar racionální funkce, dává jednoznačnou odpověď na tento problém funkce zvaná Gamma(z), jež se dá třeba snadno definovat jako limita poslounosti komplexních čísel. Pomocí ní lze velmi snadno počítat právě takové (méně příjemné, ale proto zajímavější) nekonečné součiny.
Offline
#7 16. 05. 2011 22:01
- check_drummer

- Příspěvky: 4897
- Reputace: 105
Re: Nekonečný součin
↑ Pavel:
Když tak letmo sleduji některé Tvé úpravy (i když nevidím pravé konce), nemělo by spíš být N>2L? Např. pro místa, kde do (2L)! doplňuješ součinem na N!. Díky za informaci.
"Máte úhel beta." "No to nemám."
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Nekonečný součin (TOTO TÉMA JE VYŘEŠENÉ)

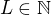 platí
platí
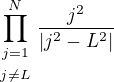 , kde
, kde  .
.![kopírovat do textarea $\Large \prod_{j=1\nlj\neq L}^{N}\,\frac{j^2}{\quad\left |j^2-L^2\right |\quad}= \prod_{j=1}^{L-1}\,\frac{j^2}{\quad\left |j^2-L^2\right |\quad}\cdot \prod_{j=L+1}^{N}\,\frac{j^2}{\quad\left |j^2-L^2\right |\quad}= \prod_{j=1}^{L-1}\,\frac{j^2}{\quad L^2-j^2\quad}\cdot \prod_{j=L+1}^{N}\,\frac{j^2}{\quad j^2-L^2\quad}=\nl =\prod_{j=1}^{L-1}\,\frac{j^2}{\quad (L-j)(L+j)\quad}\cdot \prod_{j=L+1}^{N}\,\frac{j^2}{\quad (j-L)(j+L)\quad}=\nl =\frac{1^2\cdot 2^2\cdots (L-2)^2(L-1)^2}{\quad \left[(L-1)(L-2)\cdots 2\cdot 1\right]\cdot\left[(L+1)(L+2)\cdots (2L-2)(2L-1)\right]\quad}\cdot\nl \hspace{300pt}\cdot\frac{(L+1)^2(L+2)^2\cdots(N-1)^2N^2}{\quad \left[1\cdot 2\cdots (N-1-L)(N-L)\right]\cdot\left[(L+(L+1))(L+(L+2))\cdots (L+N-1)(L+N)\right]\quad}=\nl =\frac{\left((L-1)!\right)^2}{\quad \left[1\cdot 2\cdots (L-2)(L-1)\right]\cdot\left[(L+1)(L+2)\cdots (2L-2)(2L-1)\right]\quad}\cdot \frac{(L+1)^2(L+2)^2\cdots(N-1)^2N^2}{\quad (N-L)!\cdot\left[(L+(L+1))(L+(L+2))\cdots (L+N-1)(L+N)\right]\quad}=\nl =\frac{2(L!)^2}{\quad \left[1\cdot 2\cdots (L-2)(L-1)L\right]\cdot\left[(L+1)(L+2)\cdots (2L-2)(2L-1)(2L)\right]\quad}\cdot \frac{(L+1)^2(L+2)^2\cdots(N-1)^2N^2}{\quad (N-L)!\cdot\left[(L+(L+1))(L+(L+2))\cdots (L+N-1)(L+N)\right]\quad}=\nl =\frac{2(N!)^2}{\quad (2L)!\quad}\cdot \frac{1}{\quad (N-L)!\cdot\left[(L+(L+1))(L+(L+2))\cdots (N-1)N\right]\cdot\left[(N+1)(N+2)\cdots(N+L-1)(N+L)\right]\quad}=\nl =\frac{2(N!)^2}{\quad (N)!\quad}\cdot \frac{1}{\quad (N-L)!\cdot\left[(N+1)(N+2)\cdots(N+L-1)(N+L)\right]\quad}= \frac{2N!}{\quad (N-L)!\cdot\left[(N+1)(N+2)\cdots(N+L-1)(N+L)\right]\quad}=\nl =\frac{2N(N-1)\cdots(N-L+1)(N-L)!}{\quad (N-L)!\cdot\left[(N+1)(N+2)\cdots(N+L-1)(N+L)\right]\quad} =\frac{2N(N-1)\cdots(N-L+1)}{\quad (N+1)(N+2)\cdots(N+L-1)(N+L)\quad}= \frac{2N^L+\mathcal{o}(N^L)}{\quad N^L+\mathcal{o}(N^L)\quad}. $](/mathtex/ea/eaee95822e9772d5b659ea2726dd5d1d.gif)
 do nekonečna, pak dostaneme kýžený výsledek.
do nekonečna, pak dostaneme kýžený výsledek.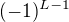 .
.