Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 25. 03. 2010 19:48 — Editoval hradecek (25. 03. 2010 19:51)
Dve exponenciálne rovnice...
Ahoj mám tu dve exp. rovnice, ktoré sa mi nedarí vypočítať...
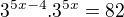

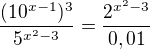
Prvú som riešil takto: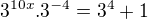
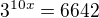
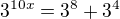
a ďalej neviem :(
Netrápte sa nad svojimi problémami s matematikou, môžem vás uistiť, že tie moje sú ešte väčšie. ~~Albert Einstein~~
Jak spozná člověk, že není pitomec ? - Moudrý člověk to nepozná nikdy a blbci je to jedno. ~~Jak přicházejí básnici o iluze~~
Někteří lidi se nikdy nezmění. Anebo se rychle změní a pak se zase rychle změní nazpátek. ~~Homer Simpson~~
Offline
- (téma jako vyřešené označil(a) hradecek)
#2 25. 03. 2010 19:57
Re: Dve exponenciálne rovnice...
↑ hradecek:
2) 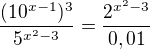
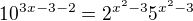
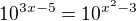
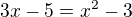

 nebo
nebo 
U 1) jseš si jistý, že máš dobře zadání?
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#3 25. 03. 2010 20:11
Re: Dve exponenciálne rovnice...
Ano zadanie mám dobre.
A v tej dvojke ako si dostal na ľavej strane 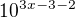 ?
?
Netrápte sa nad svojimi problémami s matematikou, môžem vás uistiť, že tie moje sú ešte väčšie. ~~Albert Einstein~~
Jak spozná člověk, že není pitomec ? - Moudrý člověk to nepozná nikdy a blbci je to jedno. ~~Jak přicházejí básnici o iluze~~
Někteří lidi se nikdy nezmění. Anebo se rychle změní a pak se zase rychle změní nazpátek. ~~Homer Simpson~~
Offline
#4 25. 03. 2010 20:29
Offline
#5 25. 03. 2010 20:32
Re: Dve exponenciálne rovnice...
↑ zdenek1:
Aha jasne.Dík
A ešte som natrafil na jednu o ktorej si mylím že nemá riešenie. Je to pravda ?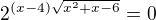
Netrápte sa nad svojimi problémami s matematikou, môžem vás uistiť, že tie moje sú ešte väčšie. ~~Albert Einstein~~
Jak spozná člověk, že není pitomec ? - Moudrý člověk to nepozná nikdy a blbci je to jedno. ~~Jak přicházejí básnici o iluze~~
Někteří lidi se nikdy nezmění. Anebo se rychle změní a pak se zase rychle změní nazpátek. ~~Homer Simpson~~
Offline
#6 25. 03. 2010 20:32
Re: Dve exponenciálne rovnice...
↑ hradecek:
pokud je 1) dobře zadání, tak budeš muset logaritmovat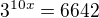 obě strany zlogaritmuješ
obě strany zlogaritmuješ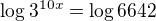

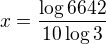
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#7 25. 03. 2010 20:41
Re: Dve exponenciálne rovnice...
↑ zdenek1:jo super.
A s touto by si mi nevedel poradiť ?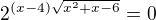
Netrápte sa nad svojimi problémami s matematikou, môžem vás uistiť, že tie moje sú ešte väčšie. ~~Albert Einstein~~
Jak spozná člověk, že není pitomec ? - Moudrý člověk to nepozná nikdy a blbci je to jedno. ~~Jak přicházejí básnici o iluze~~
Někteří lidi se nikdy nezmění. Anebo se rychle změní a pak se zase rychle změní nazpátek. ~~Homer Simpson~~
Offline
#8 25. 03. 2010 20:49
Re: Dve exponenciálne rovnice...
↑ hradecek:
Uměl, tohle nemá řešení. výraz 
Pořádek je pro blbce, inteligent zvládá chaos!
Offline

