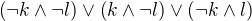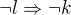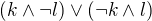Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 28. 03. 2010 14:35
výroková logika
prosím potrebujem pomôcť ohľadne výrokovej logiky, ak sa nájde nejaký ochotný človek, ďakujem vopred.
Mám výrok Príde Jana aj Eva, ale Hana nepríde. Mám to zapísané symbolicky takto :
[(p ˄ q) ˄ ¬ r]
potrebujem ale z toho urobiť negáciu, ako to bude potom zapísané?
Ďakujem moc
Offline
- (téma jako vyřešené označil(a) zdenek1)
#2 28. 03. 2010 14:56 — Editoval stepan.machacek (28. 03. 2010 14:56)
- teolog


- Místo: Praha
- Příspěvky: 3498
- Škola: MFF + PřF UK
- Pozice: Gymnázium Přírodní škola - učitel (M, Z)
- Reputace: 167
Re: výroková logika
↑ sade:
Podle pravidel výrokové logiky je negace konjunkce disjunkce negací.
Tedy ¬ [(p ˄ q) ˄ ¬ r] = ¬(p ˄ q) v r
A opět řešíme negaci konjunkce.
Tedy ¬(p ˄ q) v r = (¬ p v ¬ q) v r
Offline
#4 28. 03. 2010 18:05
- teolog


- Místo: Praha
- Příspěvky: 3498
- Škola: MFF + PřF UK
- Pozice: Gymnázium Přírodní škola - učitel (M, Z)
- Reputace: 167
Re: výroková logika
↑ sade:
Zkus to sám podle mého příkladu. Tady jsou negace všech základních složených výroků:
A a zároveň B ¬A nebo ¬B
A nebo B ¬A a zároveň ¬B
A implikuje B A a zároveň ¬B
A právě tehdy když B (A a zároveň ¬B) nebo (¬A a zároveň B)
Svůj výsledek sem napiš, ať máš jistotu.
Offline
#8 28. 03. 2010 18:31
- teolog


- Místo: Praha
- Příspěvky: 3498
- Škola: MFF + PřF UK
- Pozice: Gymnázium Přírodní škola - učitel (M, Z)
- Reputace: 167
Re: výroková logika
↑ sade:
Musíš postupovat ov "vnějších" výroků k "vnitřním".
Např. tady (¬q -> p) ˄ (q -> r) je vnější výrok konjunkce a vnitřní jsou ty dvě závorky, tedy obě implikace.
1) Nejprve znegujeme tu konjunkci. Negace konjunkce je disjunkce negací, tedy dostáváme: ¬(¬q -> p) v ¬(q -> r).
2) A teď znegujeme ty jednotliví implikace. Negace implikace (a implikuje b) je a ˄ ¬b. Takže toto aplikujeme na obě závorky a dostáváme: (¬q ˄ ¬p) v (q ˄ ¬r)
Offline
#12 28. 03. 2010 19:16
- teolog


- Místo: Praha
- Příspěvky: 3498
- Škola: MFF + PřF UK
- Pozice: Gymnázium Přírodní škola - učitel (M, Z)
- Reputace: 167
Re: výroková logika
A a zároveň B ¬A nebo ¬B
A nebo B ¬A a zároveň ¬B
A implikuje B A a zároveň ¬B
A právě tehdy když B (A a zároveň ¬B) nebo (¬A a zároveň B)
negace (¬p ˄ q) = (¬(¬p) v ¬q) = (p v ¬q)
U ostré disjunkce si nejsem jistý.
Offline
#14 28. 03. 2010 19:33
- teolog


- Místo: Praha
- Příspěvky: 3498
- Škola: MFF + PřF UK
- Pozice: Gymnázium Přírodní škola - učitel (M, Z)
- Reputace: 167
Re: výroková logika
↑ sade:
Když neguješ konjukci nebo disjunkci, tak podle výše uvedených pravidel se ta negace objeví u každé proměnné zvlášť.
¬ (A v B) = (¬ A ˄ ¬ B)
¬ (A ˄ B) = (¬ A v ¬ B)
Offline
#18 28. 03. 2010 19:54
- teolog


- Místo: Praha
- Příspěvky: 3498
- Škola: MFF + PřF UK
- Pozice: Gymnázium Přírodní škola - učitel (M, Z)
- Reputace: 167
Re: výroková logika
↑ sade:
To je špatně zapsaný, musí být buď (p ˄ q) ˄ r anebo p ˄ (q ˄ r).
Promiň, já musím zmizet. Kdybys ještě něco potřebovala, budu zpět před 23:00.
Zdar a sílu :D
Offline
#21 28. 03. 2010 22:49
- teolog


- Místo: Praha
- Příspěvky: 3498
- Škola: MFF + PřF UK
- Pozice: Gymnázium Přírodní škola - učitel (M, Z)
- Reputace: 167
Re: výroková logika
↑ sade:
Tak jsem zpět.
¬ (p -> ¬q) = (p ¬ ˄ q) špatně, má být (p ˄ q)
¬(p v r) -> q = (p v r) ˄ ¬q; pokud zadání ve skutečnosti znamená ¬[(p v r) -> q], pak to máš dobře
¬[p -> (q v r)] = [p ˄ (¬q ˄ ¬r)] dobře
¬[(r v s) -> (¬p ˄ ¬q)] = (r v s) ˄ (p ˄ q) špatně, má být (r v s) ˄ (p v q)
¬[ ¬(p ↔ r) v ¬q] = [(p ↔ r) ˄ q] dobře
Přiště zkus ty jednotlivé příklady číslovat, bude se nám v tom lépe orientovat.
Offline
#22 09. 04. 2010 09:59
Re: výroková logika
Tieto výroky sa mi zdajú zložité a neviem ako mám pri nich postupovať. Mám ich zapísať symbolicky. Ako to bude potom vyzerať?
Napr. Mám výroky : A - Do kina pôjde Katka. B - Do kina pôjde Lucia.
A potom mám výrok: Do kina pôjde aspoň jedno dievča. Bude to zapísané takto:
k v l
Ale sú ťažšie a pri nich neviem postupovať: napr.
1. Mám výrok : Do kina pôjde najviac jedno z dievčat.
2. Katka nepôjde do kina bez Lucie.
3. Do kina pôjde práve jedno z dievčat.
Ako mám potom zapísať tieto výroky?
Offline