Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 28. 03. 2010 23:01
Metodická otázka k integrálu z 1/x
Zdravím,
dneska mi během cesty vlakem vytanula na mysli následující otázka: je opravdu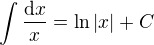 ?
?
Učí se to na středních školách a určitě i na mnoha vysokých, naleznete to v každých tabulkách (teď jsem kontroloval Bartsche)… Ale 1/x přece není funkce definovaná na celém  , primitivní funkce k ní tedy může mít tvar
, primitivní funkce k ní tedy může mít tvar
kde 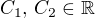 . Nic nenutí k tomu, aby platilo
. Nic nenutí k tomu, aby platilo  .
.
Co je tedy důvodem této zásadní nepřesnosti?
Offline
- (téma jako vyřešené označil(a) Olin)
#2 28. 03. 2010 23:18
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Metodická otázka k integrálu z 1/x
Pokud si dobře pamatuji, tak jsme si primitivní funkci definovali na intervalu. Pak tenhle problém odpadá a konstanta je vždy jen jedna.
Offline
#4 29. 03. 2010 11:00 — Editoval Rumburak (29. 03. 2010 11:24)
Re: Metodická otázka k integrálu z 1/x
↑ Olin:
1. Souhlas s tím, co píše kolega ↑ BrozekP:.
Vzorec
(1) 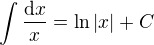
je platný na každém intervalu, který neobsahuje nulu .
2. Kolega ↑ pietro: má dozajista pravdu, pokud jde o realitu v oblastech mimo matematiku.
Pokud jde o realitu v matematice (= "virtuální realitu" v oblasti společenské hry zvané matematika), pak mám jiný názor.
Domnívám se, že "dobrá matematika" se vyznačuje tím, že tento druh reality UMÍ popsat beze zbytku.
EDIT. Po hlubším zamyšlení beru svůj poslední výrok zpět. Přesto si nemyslím, že by se tato "godelovská" otázka týkala vrorce (1).
Offline
#5 29. 03. 2010 16:53
Re: Metodická otázka k integrálu z 1/x
Děkuji za odpovědi, již je mi to jasné. Zřejmě mě vykolejila poněkud obecnější konvence značení, kterou jsme si zavedli na přednášce (str. 74).
Offline