Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 05. 04. 2010 10:28
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: kvadratická nerovnice
No musíme to vyřešeit jako kvadratickou rovnici 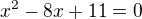 , pak víme, že parabola
, pak víme, že parabola 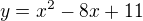 protne osu x v bodech
protne osu x v bodech 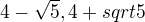 (dosazení do takového toho vzorečku s diskriminantem). No a pak jen musíme rozhodnout, která část paraboly je pod osou x. Když je u
(dosazení do takového toho vzorečku s diskriminantem). No a pak jen musíme rozhodnout, která část paraboly je pod osou x. Když je u  kladný koeficient, bude to ta mezi kořeny. Krajní body intervalu nejsou součástí řešení, protože máme ostrou nerovnost.
kladný koeficient, bude to ta mezi kořeny. Krajní body intervalu nejsou součástí řešení, protože máme ostrou nerovnost.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#4 05. 04. 2010 11:18
Re: kvadratická nerovnice
↑ leník 5: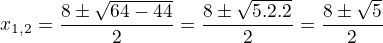
to je dobře, jen ještě zkrátit dvoju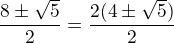
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#5 05. 04. 2010 11:39
Re: kvadratická nerovnice
↑ zdenek1: Děkuji mockrát, nenapadlo mě vytknout dvojku, to jsem tedy, co?
Offline

 výsledek má být:
výsledek má být: 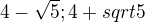 a to mně nevychází. Poradíte? Děkuji všem.
a to mně nevychází. Poradíte? Děkuji všem.