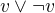Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#27 09. 04. 2010 10:58
Re: výroková logika
najviac jedno z dievčat znamená,že žiadne alebo jedna áno a druhá nie to som aj napísal
Katka nepôjde bez Lucie znamená ,že ak nepôjde Lucia tak nepôjde ani Katka to som aj napísal
práve jedno dievča znamená ,že buď pojde jedna alebo druhá niektorá musí ísť to som aj napísal
všeobecne postupovať tak,že čítať zadanie
MATH IS THE BEST!!!
Offline
#31 09. 04. 2010 18:18
Re: výroková logika
Mám slovnú úlohu :
Dievčatá išli na súťaž v plávaní. Erika nešla bez Anky. Z dvojice Anka, Mirka išla najviac jedna. Kto išiel na súťaž, keď Erika na súťaži nemohla chýbať?
Vie mi prosím niekto napísať postup ako túto úlohu riešiť - dakujem
Offline
#37 10. 04. 2010 10:44
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: výroková logika
↑ sade:
Zdravím,
tak si nastuduj, prosím "jazyk výrokové logiky" nebo i z jiných zdrojů a zkus přeložit slovní zadání do zápisů:
slovní větu (složený výrok) rozložiš na jednoduché výroky a vyznačiš spojiky mezi jednoduchými výroky.
Dievčatá išli na súťaž v plávaní. Erika nešla bez Anky. Z dvojice Anka, Mirka išla najviac jedna. Kto išiel na súťaž, keď Erika na súťaži nemohla chýbať?
jednoduchý výrok:
Erika šla, negace je "Erika nešla"
Anka šla, negace...
Mirka šla, negace...
Erika nešla bez Anky - můj překlad "Erika šla tehdy a jen tahdy, když šla Anka"
Z dvojice Anka, Mirka išla najviac jedna - můj překlad "Šla Anka nebo šla Mirka"
Erika na súťaži nemohla chýbať? - můj překlad "Erika šla".
Ted si z toho poskladej opět složený výrok:
"Erika šla tehdy a jen tahdy, když šla Anka" a zároveň "Šla Anka nebo šla Mirka" a zároveň "Erika šla". Do jazyka výrokové logiky se mi to nechce přepisovat (můžeš to zkusit a umístit sem svůj návrh), pak sestavíš tabulku, ve které najdeš řádek, kde výrok je platný.
Kolega Jarrro má naprostou pravdu, že toto je daleko rychlejší řešitelno jen po přečtení zadání (třeba u testu SCIO se těžko budeš mořit s výrokovou logikou"). Pokud byla potřeba zapsat do výrokové logiky, tak to bylo potřeba uvést přímo u zadání, a ne že být na kolegu drzá(ý).
Ať se vede.
Offline
#38 10. 04. 2010 11:36 — Editoval jarrro (10. 04. 2010 11:41)
Re: výroková logika
jelena napsal(a):
Erika nešla bez Anky - můj překlad "Erika šla tehdy a jen tahdy, když šla Anka"
Z dvojice Anka, Mirka išla najviac jedna - můj překlad "Šla Anka nebo šla Mirka"
Erika nešla bez Anky je len implikácia nie? lebo ak ide Anka tak Erika nemusí ísť platí podľa popisu len,že keď nejde Anka tak nejde Erika teda ak ide Erika tak ide aj Anka alebo ja nechápem dobre?
Anka nebo Mirka je aspoň jedna nie najviac jedna najviac jedna je podľa mňa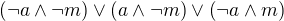
prípadne 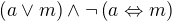
MATH IS THE BEST!!!
Offline
#39 10. 04. 2010 12:11
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: výroková logika
↑ jarrro: děkuji, určitě tomu rozumíš lépe :-)
Přečetla jsem, že podmínkou pro "šla Erika" je "šla Anka" (v implikaci by mi to znělo, že "nešla Erika" pak "nešla Anka" - tedy implikace negovaných výroků - může být?).
Nejvíc jedna (mám chybu, nezhrnula jsem variantu, že nešla ani jedna" kterou si představuji takto: 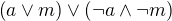 Je to tak?
Je to tak?
Vždyt povídám, že bez překladu do jazyka výrokové logiky to je rychlejší. A proto raděj to přenechám Tobě, děkuji.
Offline
#41 10. 04. 2010 14:29 — Editoval jelena (10. 04. 2010 14:29)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: výroková logika
↑ jarrro: :-) nevím :-)
Dála jsem to teď našemu synovi (bude mít 10 let), hned po přečtení vědel, že nejde Mirka. My oba ze zadání víme, že nejde Mirka - a teď poloviny soboty se budeme šmudlit s "překladem do jazyka vyrokové logiky". Já Tobě to opravdu s plnou důvěrou přenechávám, děkuji a hezky zdravím :-)
Offline
#42 10. 04. 2010 15:10
Re: výroková logika
jelena
neviem asi si necitala cele, lebo ja neviem o tom ze by som bola drza.
ja mam predmet logika, a tam to takto pisat musime - tak vysledok by som aj ja vedela ale ten zapis je problemovy. ale tak som to chcdela ako ste to vy napisali.
Offline
#43 10. 04. 2010 18:24 — Editoval jelena (11. 04. 2010 17:57)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: výroková logika
↑ sade:
Pravda, jsem na drzost trochu přecitlivá, ale ano, četla - přišlo mi, že stejné zadání opakuješ, aniž bys s Jarrro "mluvila" ve smyslu, co konkrétně potřebuješ, ale hned mu odpoviš, ať radej nereaguje. Přitom, když se podívaš na odstatní příspěvky od kolegy, tak je jasné, že řeší složité zadání a umí dobře a konkrétně poradit (někdy je trochu stručný :-)
Převod slovních formulací je vždy trochu problémový. Zkoušela jsem obě varianty pro podmínku Erika s Ankou:
a) ekvivalence  mi umožní jednoznačně zahrnout požadavek, že Erika půjde.
mi umožní jednoznačně zahrnout požadavek, že Erika půjde.
b) implikace negovaných výroků dle mého blíž se vystihuje předpoklad, že Erika na soutěži nebude, pokud nebude Anka: 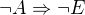 (tu jsem editovala, měla jsem původně M, ale měla být Erika)
(tu jsem editovala, měla jsem původně M, ale měla být Erika)
ohledně nejvýš jedna (Anka, Mirka) souhlasím s kolegou: 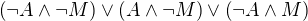 , kolegovi děkuji za upozornění.
, kolegovi děkuji za upozornění.
------
Když jsem tak uvažovala, tak z požadavku "Erika určitě půjde" mi zní, že je ještě potřeba doplnit kvantifikatory:
pro každou Eriku z množiny "Účastník soutěže" platí, že.... A to nevím, zda si nevymyšlím příliš. Věřím, že kolega to vyřeší lépe, kolegovi děkuji.
Offline
#44 11. 04. 2010 17:28
Re: výroková logika
Tak protože mne milá kolegyně jelena (zdravím) požádala, abych se na toto podíval, tak to máme takto:
Označme si výroky:
Erika šla na soutěž 
Anka šla na soutěž 
Mirka šla na soutěž 
Nyní máme premisy:
Erika nešla bez Anky. (to znamená, že pokud šla Erika, tak šla i Anka) - formálně 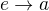
Z dvojice Anka, Mirka išla najviac jedna. (to znamená alespoň jedna nešla) - formálně 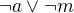
Erika na súťaži nemohla chýbať. (To znamená Erika šla) - formálně 
Teď už je to jen odvozování z těcho premis. Bohužel nevím, jaký způsob používáte. Tak jako tak, výsledek je to, co zde kolegové píšou. To znamená, že z toho vyplývá 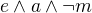
Dva jsou tisíckrát jeden.
Offline