Matematické Fórum

Alesak · 09. 03. 2008 10:11 — Editoval Alesak (09. 03. 2008 12:53)

zdravim vsechny,
letos budu maturovat, tak hadam ze me tu jeste hodnekrat uvidite;)

mam problem vyresit nasledujici rovnici:
$\sum_{n=1}^{\infty} sin^2(n-1)x = 2 tg x$

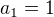takle presne to je v zadani(polak, stredoskolska matematika v prikladech 2. dil). v reseni je napsano ze $q = sin^2x$ a $a_1 = 1$ , ale ja nemuzu najit zpusob jak se k tomu dostat, spis bych rek ze a1 = x a q nevim cemu. je mozny ze to je spis chyba tisku?

jelena · 09. 03. 2008 12:09 — Editoval jelena (09. 03. 2008 13:08)

↑ Alesak:

Urcite je zadani v poradku - nema byt (n-1) v mocnine nad sin? Mocnina 2(n-1)?? Pak by to davalo smysl, jeste n by melo zacinat od 1, ale to je zrejme preklep pod znakem sumy.

$\sum_{n=1}^{\infty} sin^{2(n-1)}x = 2 tg x$ ?

Alesak · 09. 03. 2008 13:11

hmm, v knizce to je jak sem napsal, ale nejspis to bude preklep.

spravne to je asi $\sum_{n=1}^{\infty} sin^{2(n-1)}x = 2 tg x$

coz se rovna $\sum_{n=1}^{\infty} (sin^2x)^{n-1} = 2 tg x$

z cehoz vyleze $\frac1{1 - sin^2 x} = 2 tg x$

a po uprave $sin 2x = 1$

puvodne sem si myslel ze to je preklep, ale nebyl sem si jistej jestli s tim nejde neco delat. dik.

Marian · 09. 03. 2008 14:30 — Editoval Marian (09. 03. 2008 14:33)

↑ Alesak:

Chceme-li scitat nekonecnou geometrickou radu, musi byt splnena podminka, ze jeji kvocient q splnuje vztah |q|<1. V tomto pripade je

q=(sin(x))^2.

Resime tedy nerovnici

|sin(x)|^2<1.

Z vlastnosti funkce sin(x) vime, ze budou "prekazet" pouze hodnoty x takove, ze sin(x)=1 nebo sin(x)=-1. Tyto hodnoty x je treba vyloucit (pro snadnost prenechavam zajemci). Pro vsechny zbyvajici hodnoty x je pak mozne pouzit znamy vzorec pro soucet nekonecne rady, jak je uvedeno vyse. Nyni lze resit zadanou rovnici.

Pro vyloucene hodnoty x je pak zapotrebi zkoumat konvergenci rady puvodni. V obou pripadech bude ale divergovat (dostaneme totiz formalne soucet 1+1+1+...).

Dale bych chtel upozornit na to, ze lze secist i radu

$\sum_{n=1}^{K}\sin ^2((n-1)x),\qquad K\in\mathbb{N}.$

Navic plati

$\sum_{n=1}^{K}\sin ^2((n-1)x)=\sum_{n=1}^{K-1}\sin ^2(nx)=\sum_{n=1}^{K-1}\frac{1}{2}(1-\cos (2nx))= \frac{1}{2}\sum_{n=1}^{K-1}1+\frac{1}{2}\sum_{n=1}^{K-1}\cos (2nx).$

Posledni rada se pak da pro kazde prirozene K secist v uzavrenem tvaru (predevsim pak pomoci metod koplexni analyzy, coz spada absolutne mimo ramec matematiky SŠ). Limitnim prechodem K --> +oo bychom pak dostali (existuje-li v zavistlosti na x) soucet nekonence rady v zadani. Tato rada vsak bude skoro vsude divergovat, jak je patrno z vlastnosti goniometricke funkce cos(x).

Osobne se priklanim k preklepu, jak jiz bylo uvedeno. Mnou uvedena informace je tedy spise pro zajmece o reseni ulohy uvedene v puvodnim prispevku #1.

Alesak · 09. 03. 2008 14:48

dik. kdyz uz sme u tech rad, zajimalo by me, existuje nejakej lepsi a obecnejsi zpusob jak pro prvnich n cisel secist skoro libovolnou radu? treba pro $\sum_{k=1}^{n}k^2$ , sem nasel odvozeni tady, ale neslo by to nejak obecnejs? a co treba n^3 nebo 2^n? da se to nejak stredoskolsky resit?

Marian · 09. 03. 2008 15:04

$\sum_{k=1}^{n}2^k$ ... konecna geometricka rada

$\sum_{k=1}^{n}k^3=\left (\frac{n(n+1)}{2}\right )^2=\left (\sum_{k=1}^{n}k\right )^2$ ... odvozeni je o neco tezsi nez v pripade sumandu k^2, ale da se provest. SŠ metody jsou trochu tezkopadne. Na VŠ je to lepsi; v nejvetsi obecnosti lze totiz uvazit platnost tzv. Euler-Maclaurinovy sumacni formule.

Matematické Fórum

#1 09. 03. 2008 10:11 — Editoval Alesak (09. 03. 2008 12:53)

nekonecna geometricka posloupnost se sinem

#2 09. 03. 2008 12:09 — Editoval jelena (09. 03. 2008 13:08)

Re: nekonecna geometricka posloupnost se sinem

#3 09. 03. 2008 13:11

Re: nekonecna geometricka posloupnost se sinem

#4 09. 03. 2008 14:30 — Editoval Marian (09. 03. 2008 14:33)

Re: nekonecna geometricka posloupnost se sinem

#5 09. 03. 2008 14:48

Re: nekonecna geometricka posloupnost se sinem

#6 09. 03. 2008 15:04

Re: nekonecna geometricka posloupnost se sinem

Zápatí