Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 11. 04. 2010 20:20
Pohyb po krivke
Ahojte,
jednoduchý problém: Máme kĺzačku (napríklad peknú rovnú). Teleso je hore, pustíme ho a chceme rovnicami popísať jeho polohu v čase.
-
-
-
-
-
-
-
-
V tomto prípade by to nemal byť problém. Ak by to však malo tvar paraboly
-
-
-
-
-
-
-
Tak tam vychádza dlhé integrovanie. Neviem si ani predstaviť, že by kĺzačka mala netriviálny tvar. Možno ale na to idem zložito. Máme nejaký materiál, ktorý to rozoberá?
Vďaka :-)
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
- (téma jako vyřešené označil(a) lukaszh)
#2 12. 04. 2010 16:06
Re: Pohyb po krivke
↑ lukaszh: Myslim, ze v homogennom gravitacnom poli by sa to malo spravat ako stavova velicina.. to zn. ze integraly by nemali zavisiet od tvaru trajektorie....ale len od pociat. a konc stavu. co sa tyka energie
Offline
#3 13. 04. 2010 04:59 — Editoval medvidek (13. 04. 2010 05:02)
Re: Pohyb po krivke
Poznámka od ↑ pietro: je základom pre ďalšie úvahy.
Je to vidieť napríklad v prvej časti úlohy o brachystochrone http://cs.wikipedia.org/wiki/Brachystochrona .
Zo vzťahu pre čas  potrebný na prejdenie z bodu
potrebný na prejdenie z bodu  do bodu
do bodu  po obecnej klesajúcej krivke sa dá tušiť, že vyjadrenie
po obecnej klesajúcej krivke sa dá tušiť, že vyjadrenie  a
a  nebude vo väčšine prípadov triviálne
nebude vo väčšine prípadov triviálne .
.
Skúsil som to s parabolou  i s parabolou
i s parabolou  , ale nedopracoval som sa k ničomu peknému.
, ale nedopracoval som sa k ničomu peknému.
Offline
#4 13. 04. 2010 09:04
Re: Pohyb po krivke
↑ pietro: ↑ medvidek:
Vďaka za rady.
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#5 13. 04. 2010 14:38 — Editoval Rumburak (13. 04. 2010 17:20)
Re: Pohyb po krivke
↑ lukaszh:
Jde o tzv. pohyb s vazbou. Křivka K, po níž těleso klouže, nechť je popsána rovnicí y = f(x), kde f je (pro jednoduchost) klesající funkce.
V bodě T = [x, f(x)] křivky K se vektor (0, -g) tíhového zrychlení rozkládá do své tečné a normálové složky vzhledem ke křivce K.
Nechť tedy  , kde
, kde  ,
,  jsou po řadě tečná a normálová složka vektoru
jsou po řadě tečná a normálová složka vektoru  .
.
Pak  ,
, 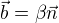 , kde
, kde  ,
,  jsou po řadě tečný a normálový vektor křivky K v bodě T. Potom
jsou po řadě tečný a normálový vektor křivky K v bodě T. Potom  . (využili jsme kolmost vektorů
. (využili jsme kolmost vektorů  ,
,  ), odtud
), odtud  .
.
Pokud zanedbáme tření, pak na pohyb bude mít vliv pouze tečná složka tíhového zrychlení , což pro Tebe jistě nebude problém vyjádřit pomocí funkce f a její derivace v bodě T.
, což pro Tebe jistě nebude problém vyjádřit pomocí funkce f a její derivace v bodě T.
V každém bodě křivky K je tak definováno zrychlení, které zde bude na těleso působit ve směru jeho dráhy, a možno tedy sestavit
pohybovou rovnici tělesa s ohledem na tuto vazbu. Jsou-li navíc dány vhodné počáteční podmínky, je tím pohyb tělese určen po celé dráze.
Jestliže bychom uvažovali i tření, byla by pohybová rovnice příslušným způsobem složitější.
EDIT. Může se stát, že se klouzající těleso setrvačností "odlepí" od křivky, je-li tato v určitém svém úseku konkávní. Řešit, za jakých okolností
se tak stane, je docela zajímavá a ne úplně snadná úloha.
Teorie pojednávající o těchto věcech se nazývá analytická mechanika a souvisí úzce s diferenciální geometrií a tensorovým počtem.
Offline
#6 13. 04. 2010 15:16
Re: Pohyb po krivke
↑ Rumburak: Nech je trajektoria napr. polkruznica, mali by sme potom dostat vztahy zhodneho tvaru so vztahmi pre matematicke kyvadlo. Odkaz
Offline
#8 13. 04. 2010 17:58 — Editoval lukaszh (13. 04. 2010 20:18)
Re: Pohyb po krivke
↑ Rumburak:
Ďakujem. Ak by som chcel súradnice v závislosti od času ![kopírovat do textarea $[x_t,y_t]$](/mathtex/f0/f0346ff57fbdc183df1db1b8401bd10d.gif) , tak by som postupoval:
, tak by som postupoval:
Z tvojho vzťahu pre zrýchlenie![kopírovat do textarea $\vec{a}=\frac{-g\frac{\rm{d}f(x_t)}{\rm{d}x_t}}{1+\[\frac{\rm{d}f(x_t)}{\rm{d}x_t}\]^2}\cdot\begin{bmatrix}1\nl\frac{\rm{d}f(x_t)}{\rm{d}x_t}\end{bmatrix}$](/mathtex/96/9658eed49095f7c7448f1373d0305410.gif)
Toto je v smere pohybu. Zo zrýchlenia v smere x a y zvlášť máme rovnice![kopírovat do textarea $\frac{\rm{d}^2x_t}{\rm{d}t^2}=\frac{-g}{1+\[\frac{\rm{d}f(x_t)}{\rm{d}x_t}\]^2}\cdot\frac{\rm{d}f(x_t)}{\rm{d}x_t}\nl\frac{\rm{d}^2y_t}{\rm{d}t^2}=\frac{-g}{1+\[\frac{\rm{d}f(x_t)}{\rm{d}x_t}\]^2}\cdot\[\frac{\rm{d}f(x_t)}{\rm{d}x_t}\]^2$](/mathtex/db/db154dafa1ec8c384323780204f72486.gif)
Je to tak?
-------------------------------------------------
Keby som to robil pre krivku - parabolu
Na počiatku je teleso v bode [0,1]. Potom máme rovnice![kopírovat do textarea $\frac{\rm{d}^2x_t}{\rm{d}t^2}=\frac{-g}{1+\[2x_t-2\]^2}\cdot[2x_t-2]\nl\frac{\rm{d}^2y_t}{\rm{d}t^2}=\frac{-g}{1+\[2x_t-2\]^2}\cdot\[2x_t-2\]^2$](/mathtex/5e/5e639e17f56a7fd78eff46631de3317f.gif)
Toto sa mi ale nezdá dobre riešiteľné. Vezmúc jednoducho triviálnu krivku
máme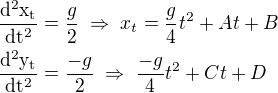
Z počiatočných podmienok vypočítame konštanty. Je to tak?
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#9 13. 04. 2010 19:17 — Editoval medvidek (13. 04. 2010 19:20)
#10 13. 04. 2010 19:28
Re: Pohyb po krivke
↑ pietro:, ↑ Rumburak:
Lenže pri pohybe po celej polkružnici už zďaleka nemôžeme použiť aproximáciu pre malé amplitúdy  , takže ↑ lukaszh: nebude mať radosť z jednoduchého elegantného riešenia :-)
, takže ↑ lukaszh: nebude mať radosť z jednoduchého elegantného riešenia :-)
Zaujímavé by bolo hľadať taký tvar krivky, aby riešenie pohybovej rovnice viedlo k dokonale harmonickým kmitom i pre veľké amplitúdy bez aproximácie. Potom by ale bolo na mieste upresniť, ČO vlastne má byť harmonické. Môže to byť x-ová súradnica telesa, ale mohla by to byť i poloha telesa meraná dížkou krivky. A vlastne i pre harmonický pohyb v y-súradnici by mala existovať nejaká krivka. Alebo sa mýlim?
Offline
#11 13. 04. 2010 20:17
Re: Pohyb po krivke
↑ medvidek:
Áno, škriatok sa mi tam dostal. Opravené :-)
↑ medvidek:
Po pár výpočtoch som zdesený z toho, že tak jednoduchú vec možno riešiť tak zložito, respektíve nejde riešiť vôbec.
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#12 13. 04. 2010 23:26 — Editoval BrozekP (13. 04. 2010 23:29)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Pohyb po krivke
↑ medvidek:
Omlouvám se, pokud můj příspěvek bude mimo, diskuzi jsem jenom v rychlosti prolétl. Vidím, že tu řešíte kmity, tak jsem jen chtěl poznamenat, že zajímavé je cykloidální kyvadlo, kde perioda kmitů nezávisí na počáteční výchylce. Pokud si dobře pamatuji, tak na rozdíl od matematického kyvadla se dá dobře analyticky řešit.
Edit: Tady (strana 44) je asi přímo odvození.
Offline
#13 14. 04. 2010 00:03 — Editoval rughar (14. 04. 2010 00:06)
Re: Pohyb po krivke
↑ medvidek:
Zdravím. Dovolil bych si zareagovat na tvůj následující integrál
Není mi zde jasné, co má znamenat to y_a. Předpokládám, že jsi vyšel ze zákona pro zachování energie
Pokud tvůj začátek vypadal stejně, jen jsi levou stranu volil jako g(y_a - y) ... , pak ses dopustil chyby. Je nutné tam nechat jen y, když pak za samotné y dosazuješ hodnoty v mezích. Víš jak to myslím? Ono to taky pak výjde hodně jinak. Bude se ti tam plést záhadný parametr y_a. Integrál ve (podle mne snad) správné formě má vypadat
Ten totiž pro parabolu řešitelný je (nedává žádne eliptické integrály jak tomu bylo u tebe). Pravda nijak zvlášť dobře, protože pak nejde udělat inverze, ale celkem se dá.
Potom bych si ještě dovolil nadhodit jednu věc do diskuse. Rovnici pro zachování energie mužeme upravit takto (jen si ještě dovolím uvažovat pro jednoduchost hmotnost tělesa m = 1)

Pak můžeme definovat

Pokud chceme vědět, pro jakou trajektorii se bude těleso chovat jako harmonický oscilátor, stačí za "naši" potenciální energii V dosadit potenciál harmonického oscilátoru. Pokud bychom chtěli něco jiného, stačí prostě jen dosadit příslušný potenciál a je to. Upravíme trochu rovnici pro potenciál

Pokud dosadíme za V potenciál harmonického oscilátoru V = ky^2, pak dostaneme poměrně dost složitý výraz![kopírovat do textarea $x=\frac{2 \sqrt{ky (g-ky)}+g ArcTan[\frac{-g+2ky}{2 \sqrt{ky(g-ky)}}]}{2k}+c$](/mathtex/cf/cf12d14229f39f2c3837338ffcc82cbf.gif)
No a to je přece krásný výsledek. Proč? Jako správní matematici všichni víme, že platí
Takže si náš výsledek můžeme uprvit na tvar![kopírovat do textarea $x=\frac{2 \sqrt{ky (g-ky)}+g ArcTan[\frac{g-2ky}{g}] - \frac{\pi g}{2}}{2k}+c$](/mathtex/29/29c04fec3079abe2aaceaa2cb1882101.gif)
A konstantu můžeme schovat do c, čili![kopírovat do textarea $x=\frac{2 \sqrt{ky (g-ky)}+g ArcTan[\frac{g-2ky}{g}]}{2k} +c$](/mathtex/f6/f6f7800d4fa6f03a9f169c62a30a3853.gif)
A u tohoto nádherného výsledku už každý správný geometr jásá, protože v něm vidí rovnici cykloidy:-).
http://cs.wikipedia.org/wiki/Cykloida
Po editaci : A taky to pochopitelně můžete odvodit podobně jak navrhnul Pavel v tom studiním textu, kde je to asi tisíckrát tak názornější :-). Koneckonců, alespoň jsem si pohrál s postupem, jak se dopracovat k výsledku pro jakýkoliv potenciál se nám zamane.
1 + 1 = 1 + 1
... a nebo taky ne
Offline
#14 14. 04. 2010 00:16
Re: Pohyb po krivke
Dovolím si napsat nový příspěvek.
Ve svém odvození jsem udělal chybu. Tady

V tomto kroku na levé straně již nebude energie, ale něco co evidntně už konstanta není. Dokážete někdo vysvětlil, jak je možné, že i přes tuto chybu je závěrečný vztah dobře? Bod reputace pro výherce. (doufám že moc nespamuji)
1 + 1 = 1 + 1
... a nebo taky ne
Offline
#15 14. 04. 2010 03:30
Re: Pohyb po krivke
↑ BrozekP:
Ďakujem za poznámku a odkazy o cykloidálnom kyvadle.
Mimochodom, spomenul som si pri tom na jednu úlohu, v ktorej sa uvažovalo o priamom tuneli spájajúcom dve ľubovoľné miesta na povrchu Zemegule. Počítal sa tam čas preletu telesa týmto tunelom za predpokladu nulového trenia a nulovej počiatočnej rýchlosti telesa. Výsledkom bolo, že tento čas je nezávislý na dĺžke tunela (rádovo 1 hodina). Jedná sa vlastne tiež o oscilátor, ktorý je tvorený telesom pohybujúcim sa v gravitačnom potenciáli vo vnútri Zeme.
Offline
#16 14. 04. 2010 04:24 — Editoval medvidek (14. 04. 2010 04:32)
Re: Pohyb po krivke
↑ rughar:
Vezmime teda vzťah, ktorý považuješ za správnejší .
.
A teraz si napríklad predstavme, že teleso začne klesať po trajektórii 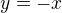 z bodu
z bodu  do bodu
do bodu  .
.
Ako sa vypočíta čas  potrebný na presun z A do B?
potrebný na presun z A do B?
A dostaneme to isté, keď zvolíme  a
a  ? Jedná sa predsa o rovnakú vzdialenosť medzi A a B, pričom klesanie je všade rovnaké.
? Jedná sa predsa o rovnakú vzdialenosť medzi A a B, pričom klesanie je všade rovnaké.
Offline
#17 14. 04. 2010 10:59
Re: Pohyb po krivke
↑ medvidek:
Myslím, že pokud jde o tvar křivky, po které by byl pohyb harmonický pro  -ovou souřadnici, tak je to parabola typu
-ovou souřadnici, tak je to parabola typu 
Potenciální energie bude  a pokud označíme
a pokud označíme  , tak
, tak  , což je přesně pot. energie pro harmonický oscilátor.
, což je přesně pot. energie pro harmonický oscilátor.
Jinak to je přesně to, co se dělá u matematického kyvadla pro malé kmity. Nahrazuje se kruhový oblouk parabolickým.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#18 14. 04. 2010 11:08
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Pohyb po krivke
↑ zdenek1:
I když to na první pohled tak vypadá, není to tak. Potenciální energie je sice  , ale kinetická je
, ale kinetická je  . To asi nevede na harmonické kmity.
. To asi nevede na harmonické kmity.
U matematického kyvadla se nenahrazuje kruhový oblouk parabolickým. Přesně u matematického kyvadla dostáváme kinetickou a potenciální energii:
Co děláme je to, že potenciál v minimu aproximujeme parabolou.
Offline
#19 14. 04. 2010 11:21 — Editoval Rumburak (15. 04. 2010 11:11)
Re: Pohyb po krivke
↑ lukaszh:
Mně také připadá, že je to správně.
V podobných úlohách bývá někdy výhodné parametrizovat křivku délkou s jejího oblouku, kde  ,
,
odpovídajícím způsobem při parametrickém popisu křivky.
Výhodou tohoto postupu je, že zrychlení v tečném směru pak můžeme vyjádřit jako skalární funkci a(s) a pohybovou rovnici (je-li možno ji takto
nazvat) pak získáme v "jednorozměrném" tvaru
(1) s'' = a(s). (derivuje se zde podle času)
Nevýhodou zde je, že neodhalíme "katastrofy" spočívající v tom, že těleso někde setrvačností "nadskočí". Ale v případech, kdy křivka je grafem
konvexní funkce, takové situace ze zřejmých důvodů nehrozí.
EDIT .
↑ zdenek1:, ↑ medvidek:
Z rovnice (1) je patrné, že aby řešením byly harmonické kmity (při nichž výchylku měříme délkou oblouku), musí být při vhodné volbě počáteční
hodnoty "oblouku" splněna identita  , kde q je kladná konstanta. Na základě této podmínky možno určit vhodné křivky.
, kde q je kladná konstanta. Na základě této podmínky možno určit vhodné křivky.
Offline
#20 14. 04. 2010 11:45
Re: Pohyb po krivke
↑ BrozekP:
Tak jsem zase o něco vzdělanější.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#21 14. 04. 2010 12:38 — Editoval BrozekP (14. 04. 2010 13:01)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Pohyb po krivke
Pro zajímavost uvedu graf závislosti výchylky  (první graf) a vodorovné složky rychlosti
(první graf) a vodorovné složky rychlosti  (druhý graf) na čase pro kyvadlo
(druhý graf) na čase pro kyvadlo  (v metrech). Těleso je puštěné nulovou rychlostí s počáteční výchylkou
(v metrech). Těleso je puštěné nulovou rychlostí s počáteční výchylkou  . Pro
. Pro  by se kmity blížily harmonickým kmitům.
by se kmity blížily harmonickým kmitům.
↑ rughar:
K tomu  . Medvidek použil značení jako je na wikipedii, tedy
. Medvidek použil značení jako je na wikipedii, tedy 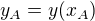 . Ty rovnou předpokládáš, že
. Ty rovnou předpokládáš, že 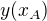 je nulové. Na výsledku to podle mě nemůže nic změnit, když se se vším správně zachází.
je nulové. Na výsledku to podle mě nemůže nic změnit, když se se vším správně zachází.
Offline
#22 14. 04. 2010 14:22 — Editoval Rumburak (14. 04. 2010 14:25)
Re: Pohyb po krivke
↑ zdenek1:, ↑ medvidek:
Jakýsi námět k úvahám o podmínkách , při nichž klouzavý pohyb po křivce v gravit. poli je harmovický,
jsem umístil do svého předchozího příspěvku ↑ Rumburak:
(nechtěl jsem porušit kontinuitu s ostatním textem).
Offline
#23 14. 04. 2010 19:00
Re: Pohyb po krivke
↑ Rumburak:
OK, ďakujem za čas. To som netušil, že táto téma vzbudí taký záujem. I keď omnoho nad rámec mojej otázky. Ale ďakujem všetkým za odpovede.
Vyřešeno
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#24 20. 04. 2010 14:57 — Editoval Rumburak (22. 04. 2010 09:28)
Re: Pohyb po krivke
↑ lukaszh:
Jak jsem si vyzkoušel, výpočet vychází podle mě docela zajímavě a hezky pro hyperbolickou dráhu y = 1/x , x > 0.
EDIT. Ale poté, kdy jsem ve svých výpočtech objevil chybu, si to už nemyslím. ...
Offline

![kopírovat do textarea $\[2x_t-1\]$](/mathtex/d8/d898a9b12c56430d3edab06ecb97d133.gif) , kde by malo byť
, kde by malo byť ![kopírovat do textarea $\[2x_t-2\]$](/mathtex/33/33049342e0d148ceee06bdc75f7ae96a.gif) .
.