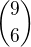Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 13. 04. 2010 19:29
Kombinatorika
Ahoj, mam tu nekolik prikladu u kterych delam asi chybu a nemuzu prijit na to jakou. Predem dekuji za pomoc
1) Mame cislece 0,1,2,3,4,8,9
a) kolik cislic muzeme sestavit pokud se cisla nemohou opakovat a cisla jsou peticiferna a licha
b) cislice se mohou opakovat a cislo je vets nez 300 a mensi nez 80000?
2) Mame sadu hracich karet- 4 barvy a 8 vysek
a) kolika zpusoby muzeme vybrat ze sady 6karet jestlize rozlisujeme karty pouze podle barvy
b) kolika zpusoby muzeme seradit vsechny karty do rady, tak aby karty stejne vysky byly vedle sebe?
3) Mame 12 ruznych jednohodinovych a 4 ruzne dvouhodinouve predmety, mezi jednohodinovymi je matematika, mezi dvouhodinovymi matematicka cviceni
a) kolika zpusoby lze sestavit rozvrh na jeden den se sedmi hodinami, ma-li obsahovat pouze jeden dvouhodinovy predmet?
b) kolika zpusoby muzeme sestavt rozvrh na jeden den, ktery ma sedm hodin a maji v nem byt alespon 2 dvouhodinove predmety?
Offline
- (téma jako vyřešené označil(a) zdenek1)
#3 13. 04. 2010 21:28
Offline
#4 14. 04. 2010 08:16 — Editoval septolet (14. 04. 2010 08:26)
Re: Kombinatorika
↑ zdenek1: Můžu se zeptat, proč u 1a vybíráš nejprve z 5 čísel? A ty poslední dvě pozice mi také nejsou jasné. Já bych to spíše viděl na (6*6*5*4*3)/2. Nejprve mám 6 čísel, pak také 6, předchozí pozice - 1 číslo, ale zase + ta 0, takže opět 6) a pak s každou pozicí jedno číslo odeberu. A jelikož liché číslo je každé druhé, tak bych to vydělil 2. Podle mě by tedy vyšlo 1080. Takže kde případně uvažuji špatně? Děkuji.
Offline
#5 14. 04. 2010 10:48
Re: Kombinatorika
↑ septolet:
Ono je to zapsané podle pozic, na které vybírám, ale ne v pořadí, které vybírám.
Nejprve vybírám tu poslední trojku _ _ _ _ 3 (končí 1,3,9)
pak vybírám první pětku 5 _ _ _ 3 (nemůžu mít nulu na začátku a jedna cifra už je vypraná na konci)
pak druhou pěrku 5*5 _ _ *3 (mám pryč dvě ifry, ale už můžu mít nulu)
a zbytek je snad jasný
Tvůj problém je v tom, že lichých čísel není polovina. Máš 3 liché cifry a 4 sudé.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#7 14. 04. 2010 15:28 — Editoval aGr (14. 04. 2010 15:30)
Re: Kombinatorika
↑ zdenek1:
Mám pár nejasností :).
2) a) Nemělo by to býti 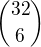 ? Nebo teda
? Nebo teda  pokud chci stejné barvy.
pokud chci stejné barvy.
b) Jen pro jistotu: 8! je uspořádání všech těch čtveřic stejných výšek, 4! je uspořádání "uvnitř" těch čtveřic a na osmou, protože to "uvnitř" musím uspořádat v každé té čtveřici?
Offline