Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 13. 03. 2008 20:46
Logaritmická nerovnice
Ahoj,
měl bych tady jeden příklad:
(x^2 -5x)logx>0
Výsledek: (0;1)U(5;+nek)
A mám tedy najít množinu všech reálných čísel...
A chtěl bych se zeptat na pár otázek, protože někde mi něco v řešení chybí:
1.) (x^2 -5x) položím větší než NULA? Ale proč? Snad kvůli tomu, že celý výraz na levé straně má být větší než NULA? A kdyby byl celý výraz menší než NULA, pokládal bych tu závorku menší než NULA?
2.) u (logx) položím x>0, tak se to myslím dělá...
Ale asik mi tu ještě něco chybí... Jelikož se mi tam někde ztratil ve výsledku interval (0;1)
-----------------------------------------------------------------------
3.) Zajímalo by mě, jak by se změnily odpovědi na tyto otázky, kdyby nebyl logaritmus při základu 10, ale byl by při základu třeba 1/2 ?
Je mi jasné, že je to takové delší, ale velmi by mi to pomohlo.
Díky moc
Offline
#2 13. 03. 2008 21:43 — Editoval plisna (13. 03. 2008 22:09)
Re: Logaritmická nerovnice
nejlepe se to udela pres tabulku:
| -oo, 0 | 0, 1 | 1, 5 | 5, oo |
==========================
x | - | + | + | + |
----------------------------------------------
x - 5 | - | - | - | + |
----------------------------------------------
log x | nelze | - | + | + |
----------------------------------------------
jestli hranicni body do intervalu patri nebo ne, se nejrychleji udela primo dosazenim. je to srozumitelne?
Offline
#3 13. 03. 2008 21:46 — Editoval jelena (13. 03. 2008 22:21)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Logaritmická nerovnice
lopson napsal(a):
(x^2 -5x)logx>0
Výsledek: (0;1)U(5;+nek)
A mám tedy najít množinu všech reálných čísel...
Množinu všech realnych cisel prece nehledas, hledas mnozinu takovych cisel patricich do oboru R, co splnuji zadanou nerovnici.
Je potreba si uvedomit, ze leva strana nerovnice je soucin, ktery bude vetsi nez 0, kdyz:
- oba cinitele jsou kladne - proto polozis jak (x^2 -5x), tak i logx vetsi nez nula, zaroven je potreba splnit podminku platnou pro x (tak, jak rikas: u (logx) položím x>0, to je spojeno s definicnim oborem pro funkci log.)
- oba cinitele jsou zaporne - nesmime ztratit a resime obdobne, urcite to zvladnes.
To jest tady se reklo: (plus krat plus dava plus, minus krat minus dava plus)
lopson napsal(a):
A kdyby byl celý výraz menší než NULA, pokládal bych tu závorku menší než NULA?
- musel bys uvedomit, za kterych podminek soucin bude zaporny (plus krat minus ....minus krat plus :-) a podminka pro x, jelikoz je za log - opet plati
Jeste bych upozornila, ze zavorka se rozlozi take na soucin, proto je idealni rovnou rozlozit na soucin a resit pomoci jedne tabulky - znamenka na intervalech.
lopson napsal(a):
3.) Zajímalo by mě, jak by se změnily odpovědi na tyto otázky, kdyby nebyl logaritmus při základu 10, ale byl by při základu třeba 1/2 ?
jedina zmena by byla v tom, ze:
funkce log se zakladem 1/2 je klesajici a nabyva kladnych hodnot pro x vetsi 0, ale mensi 1.
Naopak log x se zakladem 10 je kladna pro x vetsi 1 a zaporna pro x mensi 1 a vetsi 0.
Vim, ze je toho hodne, tak se o to pokus a ptej se dal. Hodne zdaru :-)
Editace: kolega plisna vyresil to, co jsem byla lina vypisovat - tabulku. Dekuji a zdravim :-)
Editace: dekuji kolegovi halogan za upozorneni,
mela jsem hrozny preklep u log se zakladem 10 - uz opraveno (temer neodpustitelny preklep, vymyslim si nejaky trest :-)
Offline
#4 13. 03. 2008 21:59 — Editoval halogan (13. 03. 2008 22:01)
#6 13. 03. 2008 22:19
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Logaritmická nerovnice
↑ halogan:
Dekuji za upozorneni, uz napraveno - trestuhodny preklep to byl :-)
Offline
#7 13. 03. 2008 22:20 — Editoval lopson (13. 03. 2008 22:22)
Re: Logaritmická nerovnice
Jen bych se rád akorát zeptal na tu JEDNICKU v te tabulce u Plisni. Jestli je tam z toho důvodu, že tento graf protíná osu x v bude 1? A je to tak ve všech typech logaritmickych nerovnic?
Edit: Vlastne ve vsech to asik nebude, jelikoz funkce lze posunovat. :-) Objasnil by mi to někdo trosicku?
Offline
#10 14. 03. 2008 00:15
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Logaritmická nerovnice
↑ lopson:
Dokazovat to nemusime,
ale musime si uvedomit, ze je to "nulovy bod" pro logx:
pri x = 1 bude logx =0, tj. cely soucin na leve strane nerovnice bude nulovy, coz nezapada "do nasich planu" - musi podle zadani byt vetsi nuly.
Proto, pokud 1 bude na konci nebo na zacatku intervalu, tak zde musi byt interval otevreny ("okrouhla zavorka").
Pokud jsem spravne rozumela tve otazce.
Offline
#12 15. 03. 2008 23:34 — Editoval lopson (16. 03. 2008 00:21)
Re: Logaritmická nerovnice
Ahoj,
tak jsem zkoušel pár příkladů a jen bych byl rád, kdyby mi to někdo překontroloval, jestli mám správný postup v tabulce.
Příklad:
(1)
(x^2 - 3x)log(x-2)<0
| -oo, 0 | 0, 2 | 2, 3 | 3, oo|
==========================
x | - o + | + | + |
-----------------------------------------------
x - 3 | - | - | - o + |
-----------------------------------------------
log (x-2)| nelze | nelze o - | + |
-----------------------------------------------
(+) (+)
o --> nulový bod
Vyšlo mi, že nikdy není záporný, prázdná množina
(2) - předpokládejme, že u logaritmu je základ (1/2)
(x^2 - 3x)log(x-2)<0
| -oo, 0 | 0, 2 | 2, 3 | 3, oo|
==========================
x | - o + | + | + |
-----------------------------------------------
x - 3 | - | - | - o + |
-----------------------------------------------
log (x-2)| nelze | nelze o + | - |
-----------------------------------------------
(-) (-)
Výsledek: (2,3)U(3,oo)
Jsou oba zapsány správně?
Edit: Ještě bych se chtěl zeptat --> Kdyby místo otevřeného intervalu tam byl uzavřený, projevilo by se to tak, že by byly všude hranaté závorky kromě okolí asymptot a nekonečen?
Díky...
Offline
#14 15. 03. 2008 23:52 — Editoval lopson (16. 03. 2008 10:50)
Re: Logaritmická nerovnice
Myslíš tedy až do tříí?
Edit: No mně to přijde správně (podle toho úplně prvního příkladu na začátku), ale jak vidím tak není :-)
Ted mi asik vyšlo, že "nelze" do dvou...
| -oo, 0 | 0, 2 | 2, 3 | 3, oo|
==========================
x | - o + | + | + |
-----------------------------------------------
x - 3 | - | - | - o + |
-----------------------------------------------
log (x-2)| nelze | nelze o - | + |
-----------------------------------------------
(+) (+)
Takto?
Jojo, jsem to, ale ?ulpa...
Už jsem to tam upravil, mělo by to být OK. A s temi uzavrenymi intervaly jsem mel pravdu?
Jojo, tak jsou ty zaklady myšleny.
Edit: Jop, překlep, už opraveno.
Offline
#15 16. 03. 2008 00:14 — Editoval jelena (16. 03. 2008 00:15)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Logaritmická nerovnice
↑ lopson:
Az do 2 "nelze" :-), definicni obor pro log (x-2) je (2, +oo), v intervalu (2,3) je log (x-2) zaporne, pak kladne.
Tady byl zaklad log 10, je to tak? a v tom druhem prikladu - zaklad log 1/2?
Offline
#16 16. 03. 2008 00:26 — Editoval jelena (16. 03. 2008 00:29)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Logaritmická nerovnice
↑ lopson:
Ten druhy priklad, se zakldem 1/2 bude v poradku, pokud opravis definicni obor pro log. Jinak se zda byt OK.
Hranate zavorky by byli vsude tam, kde funkce bude 0 - treba pro
x = 0 - toto ovsem nepatri do def. oboru
x = 3 - to je zajimave, jelikoz v x 3 mame jak zavorku (x-3) nulovou, tak i log(3-2) je take 0.
"Asymptota" - asi mas na mysli x=2 (to neni nulovy bod, tak neni co resit ve smyslu znamenka) - ostatne tvrdit, ze tam bude asymptota pro cele zadani funkce, to bych si netroufa, muselo by se to overit - pro nas priklad to nema zatim zadny vyznam, to jen poznamka.
Editace: jak jsi naposled upravoval reseni, tak tam zustalo (-) v poslednim radku - celkove znamenko - urcite preklep, jen pro poradek
Offline

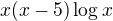 , pricemz nyni hledam "nulove body", tedy takova x, pro ktera je dany vyraz nulovy. tyto body pak "rozdeli" realnou osu na dane intervaly. ta "jednicka" plyne z logaritmu, jelikoz plati, ze
, pricemz nyni hledam "nulove body", tedy takova x, pro ktera je dany vyraz nulovy. tyto body pak "rozdeli" realnou osu na dane intervaly. ta "jednicka" plyne z logaritmu, jelikoz plati, ze 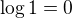 . ok?
. ok?