Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#4 26. 04. 2010 21:28
Re: Integrál
↑ Ferdish:
Nezaručujem, že postup niekam vedie. Videl som tento typ integrálu (logaritmus v kombinácií s goniometrickou funkciou) dobre riešiť pomocou parametrických integrálov. Budeme uvažovať funkciu
Zderivujme uvedenú funkciu podľa y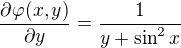
Potom pre našu pôvodnú funkciu platí rovnosť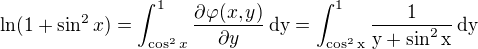
Potom máme
Teraz zameníme hranice integrovania.
Odtiaľ máme
Toto nebudem počítať, nakoľko neviem, či sa to bude dať spočítať. Ale za pokus to stojí.
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#5 26. 04. 2010 21:29
Offline
#6 26. 04. 2010 21:50 — Editoval Ferdish (26. 04. 2010 21:52)
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Integrál
Neviem, mozno je tam niekde chyba...tento integral som dostal ako medzivysledok. Povodnou ulohou bolo zintegrovat tento integral:
Riesil som per partes, za nederivovanu fciu (u) som dosadil  a za derivovanu (v') zlomok
a za derivovanu (v') zlomok  .
.
Riesenie je ![kopírovat do textarea $[\frac12t.ln(sin^2t+1)]od0po{\frac\pi2}-\frac12\int_0^{\frac\pi2}ln(sin^2t+1)dt$](/mathtex/db/db3c4b7004b314c268b66fa603fcb720.gif) , kde je zrejme ze podintegralna fcia je riesenim integracie fcie v'. A prave ten druhy clen vysledku mi robi problem.
, kde je zrejme ze podintegralna fcia je riesenim integracie fcie v'. A prave ten druhy clen vysledku mi robi problem.
Offline



