Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 25. 04. 2010 22:19
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
derivace pro Zuzanku.K
Zdravím vás,
témata zakládám velmi omezeně, ovšem dostalo se mi mailu, jehož obsah nesdělím, ale na jehož základě mám bez strojových prostředků předvést derivaci zadané funkce i s postupem.
Za nalezené chyby děkuji.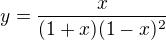
1. derivace:
máme před sebou podíl funkcí  a
a 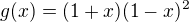 .
.
Funkce g(x) je součínem funkce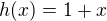 a složené funkce
a složené funkce 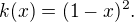 A tak k tomu budu i přistupovat při derivování:
A tak k tomu budu i přistupovat při derivování: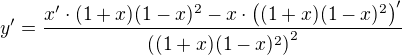
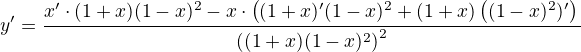
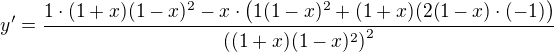
Vím, že v souladu s doporučením kolegy Olina bych měla převest podíl na součín, ale nechám to tak. Také jsem neotvírala závorky, ale pokud bude potřeba, samozřejmě otevřu i závorky.
Také případně vysvětlím i nejasné kroky v postupu.
OT: podělím se o svou odpověd na jiný mail. Je to můj názor, který mohu stejně dobře sdělit v mailu, tady na fóru nebo na Horním náměstí v Opavě.
Jelena ve svém mailu napsal(a):
Co se tyče profesorů z katedry - my to naopak velmi podporujeme, že čtou a pomáhají.
My za to velmi děkujeme. Pokud uvidí alespoň nějaký návrh řešení nebo smysluplný konkrétní dotaz, tak budou diskutovat a navedou.
Doporučovala bych na fórum v tomto smyslu umístit.
"umístit dotaz"- pro upřesnění (bylo to v kontextu).
Velmi se omlouvám za použití množného čísla, nevím, zda mám právo mluvít i za někoha dalšího z kolegů. Tak jsem asi psat neměla.
Děkuji.
Offline
- (téma jako vyřešené označil(a) jelena)
#2 26. 04. 2010 09:58
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: derivace pro Zuzanku.K
Použila jsem 4 povinné dotazy k řešení problému a svůj problém vyřeším následovně:
Otvírám závorky: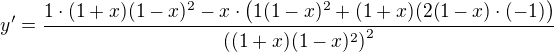
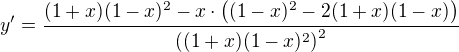

![kopírovat do textarea $y^{\prime}=\frac{(1-x)\[(1+x)(1-x)-x(1-x)+2x(1+x)\]}{\((1+x)(1-x)^2\)^2}$](/mathtex/3f/3f48b1bfad1133be8628c4cc3214e15e.gif)
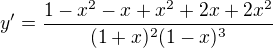
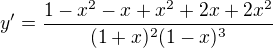

abychom dostali výsledek z MAW, je třeba upravit závorku v jmenovateli 
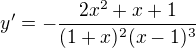
Jsou případně další dotazy k tomuto tématu?
Neboť je jaro a je třeba vyhnat zebry na pastvu.
------------------------------------------------------------------------------------
A zcela OT: kdo z kolegů se ještě účastnil předmětné dotazníkové akce? Děkuji a zdravím.
Offline
#4 28. 04. 2010 21:25 — Editoval Krezz (28. 04. 2010 21:27)
Re: derivace pro Zuzanku.K
↑ zuzanka.k:
Zdravim
Dovolim si odpovedet za kolegini. Na ctvrtou tam neni protoze z citatele vytkla 1-x ktere zkratila s tim v jmenovateli.![kopírovat do textarea $y^{\prime}=\frac{(1-x)\[(1+x)(1-x)-x(1-x)+2x(1+x)\]}{\(1+x)^2(1-x)^4}$](/mathtex/e4/e4f4e81ca238da47ac62f37e96372a25.gif)
Tady by to melo byt zhrejme
Offline
#6 29. 04. 2010 22:43
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: derivace pro Zuzanku.K
↑ zuzanka.k:
Další derivace - derivujeme výsledek 1. derivace, opět si uvedomíme, kde je podíl, složena funkce atd. Ať se vede.
Offline
