Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z algebry
- » Součet třetích mocnin (snadnější úloha) (TOTO TÉMA JE VYŘEŠENÉ)
#2 27. 04. 2010 18:54
Re: Součet třetích mocnin (snadnější úloha)
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#4 28. 04. 2010 18:53
Re: Součet třetích mocnin (snadnější úloha)
MATH IS THE BEST!!!
Offline
#7 29. 04. 2010 19:10
- check_drummer

- Příspěvky: 4952
- Reputace: 106
Re: Součet třetích mocnin (snadnější úloha)
Téma je sice uzavřené, přesto přispěju. :-)
Dokažme obecnější tvrzení:
pro všechna a,b,c přirozená je následující výraz dělitelný 9: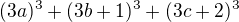
To je ale zřejmé, protože 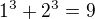 .
.
Teď už stačí jen použít fakt, že z čísel n, n+1, n+2 dávají tato čísla zbytek 0, 1, 2 po dělení 3 (ne nutně v tomto pořadí).
"Máte úhel beta." "No to nemám."
Offline
#8 29. 04. 2010 20:45
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Součet třetích mocnin (snadnější úloha)
Celkem není těžké to zobecnit:
Pro která
platí
?
Co nemám rozmyšlené je, jak by to dopadlo s dělitelností 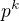 pro
pro  .
.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#9 29. 04. 2010 22:40
Re: Součet třetích mocnin (snadnější úloha)
↑ Kondr:Já myslím, že  by mělo být liché číslo. Jinak evidentně pro
by mělo být liché číslo. Jinak evidentně pro  je součet mocnin liché číslo a nemůže být dělitelné (sudým)
je součet mocnin liché číslo a nemůže být dělitelné (sudým)  .
.
Pomoci by mohlo, že když počítáme modulo  , tak
, tak  a
a 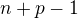 dávají zbytek
dávají zbytek  , resp.
, resp.  , po dělení číslem
, po dělení číslem  .
.
Offline
#10 29. 04. 2010 23:35
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z algebry
- » Součet třetích mocnin (snadnější úloha) (TOTO TÉMA JE VYŘEŠENÉ)

![kopírovat do textarea $\Large n^3+(n+1)^3+(n+2)^3=\left[n^3+(n+2)^3\right]+(n+1)^3=(n+n+2)[n^2-n(n+2)+(n+2)^2]+(n+1)^3=\nl =2(n+1)(n^2+2n+4)+(n+1)^3=(n+1)(2n^2+4n+8+n^2+2n+1)=3(n+1)(n^2+2n+3)$](/mathtex/63/63b90873ab700c55c91f3176b91dbac9.gif)
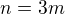 ,
, 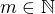 , pak je výraz v druhé závorce dělitelný třemi.
, pak je výraz v druhé závorce dělitelný třemi. ,
,  ,
,  vždy dělitelný 3. Tzn.
vždy dělitelný 3. Tzn. 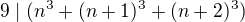 .
. teda pravda pre n+1 mame
teda pravda pre n+1 mame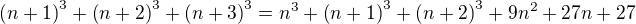 čo je
čo je . Potom máme součet třetích mocnin
. Potom máme součet třetích mocnin 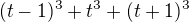 . Usnadní to úpravy v obou navrhovaných postupech.
. Usnadní to úpravy v obou navrhovaných postupech.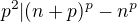 , tím je hotov indukční krok por všechna
, tím je hotov indukční krok por všechna  , kde k>0 a l je liché, si všimneme, že zbytky mod
, kde k>0 a l je liché, si všimneme, že zbytky mod 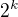 se v řadě
se v řadě 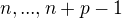 periodicky opakují, každý l-krát. Aby byla suma dělitelná
periodicky opakují, každý l-krát. Aby byla suma dělitelná  jedniček, zbytek jsou nuly.
jedniček, zbytek jsou nuly.