Matematické Fórum

Vinc · 26. 04. 2010 20:31

Prosím o pomoc

Má se určit Taylorův polynom n-tého řádu funkce f v bodě X0, je-li: f(x) = lnx , x0 = 1 , n patří do N

medvidek · 27. 04. 2010 04:23

Definice Taylorova polynomu:
$T_n = f(x_0) + \frac{f^\prime(x_0)}{1!} (x - x_0) + \frac{f^{\prime\prime}(x_0)}{2!}(x - x_0)^2 + \ \ldots \ + \frac{f^{(n)}(x_0)}{n!}(x - x_0)^n= \sum_{k=0}^n \frac{f^{(k)}(x_0)}{k!} (x-x_0)^{k}$
Derivace funkce $f(x)=ln(x)$ budou
$f^{(1)}(x)=\frac{1}{x}$
$f^{(2)}(x)=\frac{-1}{x^2}$
$f^{(3)}(x)=\frac{2}{x^3}$
$f^{(4)}(x)=\frac{-6}{x^4}$
$f^{(5)}(x)=\frac{24}{x^5}$
...
$f^{(k)}(x)=(-1)^{(k-1)} \cdot \frac{(k-1)!}{x^k}$
K-tá derivace v bodě $x=x_0=1$
$f^{(k)}(1)=(-1)^{(k-1)} \cdot (k-1)!$
Po dosazení
$T_n = ln(1)+\sum_{k=1}^n \frac{(-1)^{(k-1)} \cdot (k-1)!}{k!} (x-1)^{k}= \sum_{k=1}^n \frac{(-1)^{(k-1)}}{k} (x-1)^{k}$

Vinc · 27. 04. 2010 13:56

a čemu se teda ve výsleku bude rovnat n, resp. polynom kolikatého řádu musíme spočítat aby byl výsledek co nejpřesnější?

kaja(z_hajovny) · 27. 04. 2010 15:35

Asi to mate vypocitat pro obecne n.

Cim vetsi n, tim presnejsi vysledek pri nahrazeni funkce polynomem.

Ale v tomto pripade ta presnost vysledku roste pomalu, pro aproximaci logaritmu je lepsi pouzit ln((1+x)/(1-x)) nebo tak neco.

Vinc · 27. 04. 2010 16:21

a nemuže se stát že při dosažení určitého n se přesnost naopak začne zmenšovat?

medvidek

↑ Vinc:
Pro $x \in \left (0,2 \right >$ a zejména v blízkém okolí $x_0=1$ je tato řada konvergentní a s rostoucím $n$ roste přesnost aproximace funkce $ln(x)$ polynomem $T_n$ .

Vinc · 27. 04. 2010 19:15

Diky :)

medvidek · 27. 04. 2010 19:45

↑ Vinc:
Není zač.

↑ kaja(z_hajovny):
Myslíš jako najít rozvoj pro něco takovéto
$y = ln \left (\frac{1+x}{1-x} \right )$
a pak tam použít substituci $z=\frac{1+x}{1-x}$ resp. inverzní?

mysteriouss · 30. 04. 2010 17:40

↑ medvidek:
jak prosím příjdu na to do jakého intervalu patří X?
díval jsem se všude na internetu a nikde to není vysvětleno tak nějak polopatě :D
taky jsem našel třeba stránku čvut se spooustou řešených příkladů ale o tom jak dostat ten interval taky ani zmiňka :(
poraďte prosím

medvidek · 30. 04. 2010 20:18

↑ mysteriouss:
Lopatistická kuchařka:

Máme mocninnou řadu
$\sum_{k=0}^\infty a_k (x-x_0)^{k}$
Vypočteme limitu
$\lim_{k \to \infty} \left | \frac{a_k}{a_{k+1}} \right |=R$
Pokud tato limita existuje, hledaný interval konvergence bude $x \in \left (x_0-R;x_0+R \right)$ .
V konkrétním případě máme 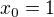$x_0=1$ , výpočtem limity dostaneme $R=1$ , z toho vychází $x \in \left (0;2 \right)$ .

Tato kuchařka neřeší konvergenci řady v krajních bodech intervalu, ale to už by neměl být problém zjistit jinak.

Základní informace o konvergenci mocninných řad najdeš např. zde
http://cs.wikipedia.org/wiki/Mocninn%C3%A1_%C5%99ada