Matematické Fórum

Zeus · 30. 04. 2010 20:46 — Editoval Zeus (30. 04. 2010 21:15)

Zdravím přátele matematiky,

kdysi, ještě na základce, nám ukázala jedna učitelka hezký trik na ověření správnosti násobení. Teď se chystám na maturitu z matiky, zdegeneroval jsem, tak na násobení používám kalkulačku :-D, ale štve mě, že tento „důkaz“ pořád absolutně nechápu.

Zde to tedy je, přeloženo do vyšší matematiky ;-):

Proč platí, že si můžu dost pravděpodobně ověřit výsledek násobení a × b = c když zkusím „ciferný součet součinu ciferných součtů činitelů = ciferný součet výsledku.“ ALE! vždy dělám „postupný“ ciferný součet až do doby, než dostanu jednociferné číslo (možná se tomuto postupu nějak říká).

Radši konkrétně.

8965 × 2156 = 19 328 540 (to mi spočítal Wolfram, fakt to tak je)

ciferný součet 8965 => 28 => 10 => 1
ciferný součet 2156 => 14 => 5
5 × 1 = 5
ciferný součet 19 328 540 => 32 => 5

5 = 5 !!!

Kdyby nevyšlo, výsledek by byl 100 % špatně.
Když vyjde, nemůžu si být stoprocentně jistý, protože kdybych prohodil číslice (třeba 19 823 504 místo 19 328 540), nepoznal bych to na součtu, ale i tak se to hodí.

Ach proč, prosím, proč? :-D Nedá mi to spát :-)

Děkuju a přeju hezký večer :-)

Zdeněk

Edit: PS: Promiňte, jen ještě taková drobnost – já vlastně neVÍM, že když to nevyjde, tak je výsledek špatně, ale za ty roky, co to používám, to ještě nikdy nezklamalo :-). Jako matematický důkaz to není úplně košer, ale… :-)

Pavel Brožek · 30. 04. 2010 21:38

Vezměme si nějaké k-ciferné číslo $n$ . To mohu obecně zapsat pomocí jeho cifer jako $n=\sum_{i=0}^{k-1}a_i\cdot 10^i$ , kde $a_i$ jsou cifry čísla $n$ . Platí

$n=\sum_{i=0}^{k-1}a_i\cdot (9+1)^i=$\sum_{i=0}^{k-1}a_i$ +9\cdot(\ldots)$ ,

číslo $n$ má tedy stejný zbytek po dělení devíti jako jeho ciferný součet. Provádíme-li tyto ciferné součty dokud nedostaneme jednociferné číslo, stále zůstává zbytek po dělení devíti stejný. Za předpokladu, že n je nenulové číslo, je dán výsledek ciferného sčítání jednoznačně zbytkem po dělení devíti (pokud je číslo dělitelné devíti dostaneme 9, jinak dostaneme přímo zbytek).

Libovolné číslo, které dává po dělení devíti zbytek $z\in\{0,1,2,\ldots,8\}$ můžeme zapsat jako $9c+z$ , kde $c$ je vhodné celé číslo. Tak se to běžně dělá, pro nás ale bude vhodnější volit $z\in\{1,2,\ldots,9\}$ , protože pak $z$ přímo představuje číslo, které dostaneme ciferným sčítáním. Vynásobíme teď dvě různá čísla s různými z:

$(9c_1+z_1)(9c_2+z_2)=9(9c_1c_2+c_1z_2+c_2z_1)+z_1z_2$

Na tento součin se podívejme z hlediska toho pravidla.

ciferný součet součinu ciferných součtů činitelů = ciferný součet výsledku.

"Opakovaný" ciferný součet prvního činitele je 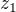$z_1$ , "opakovaný" ciferný součet druhého činitele je $z_2$ , zajímá nás tedy "opakovaný" ciferný součet jejich součinu $z_1z_2$ . Tím dostaneme zbytek po dělení $z_1z_2$ devíti (resp. 9 pokud $z_1z_2$ je dělitelné devíti). To samé ale dostaneme, pokud provedeme "opakovaný" ciferný součet pravé strany.

Zeus · 30. 04. 2010 21:51 — Editoval Zeus (30. 04. 2010 21:54)

Jo, přesně tohle je odpověď jako od Sheldona Coopera :-).

MOC děkuju, zkusím si to opravdu pořádně přečíst a strávit následujících pár hodin, dnů, týdnů… snahou to pochopit, protože to vypadá geniálně :-)

Ale vážně, náhodou myslím, že to začínám chápat! JE to geniální! Děkuju moc! Ještě si to párkrát přečtu (tak 100×), abych se ujistil, že jsem to vážně pochopil, ale vypadá to úžasně chytře a přesto ve své podstatě jednoduše (byť bych na to NIKDY sám nepřišel)!

PS: Je toto běžný/praktický/pohodlný způsob kontroly výsledku? :-)

Ještě jednou děkuju!

Edit: Ha, už jsem se zasekl, s dovolením si to trochu rozrýpu v další reakci.

Zeus · 30. 04. 2010 22:12 — Editoval Zeus (30. 04. 2010 22:18)

BrozekP napsal(a):
Vezměme si nějaké k-ciferné číslo $n$ . To mohu obecně zapsat pomocí jeho cifer jako $n=\sum_{i=0}^{k-1}a_i\cdot 10^i$ , kde $a_i$ jsou cifry čísla $n$ .

To je geniální zápis. A kupodivu ho i chápu.

BrozekP napsal(a):
$n=\sum_{i=0}^{k-1}a_i\cdot (9+1)^i=$\sum_{i=0}^{k-1}a_i$ +9\cdot(\ldots)$

,

První problém – já věřím, že to tak je, ale proč? (Stačí samozřejmě obecně - vyplývá to z nějakých pravidel počítání se sumou? Že když násobím vnitřek konstantou, tak ji můžu ze sumy „vyndat“ - přičíst - nebo něco v tom smyslu? Pokud ano, stačí napsat „Jsou na to pravidla“ a já si je nastuduji, v tom mám mezery, která rád zaplním.

Vytknutí devítky před závorku mi dalo zabrat, ale ano, myslím, že to mám. Dá se to chápat tak, že v závorce (…) je nějaké číslo, třeba „m“, které NENÍ beze zbytku dělitelné devíti?

Autor skryl část textu. Zobrazit/skrýt!

EDIT: Tady vlastně ale nejdou neznámé - takže jsem napsal blbost. vždy mi zbyde „1“ ( $x=1$ ), akorát $g$ bude růst, když bude růst $i$ , ne?

BrozekP napsal(a):
číslo $n$ má tedy stejný zbytek po dělení devíti jako jeho ciferný součet. Provádíme-li tyto ciferné součty dokud nedostaneme jednociferné číslo, stále zůstává zbytek po dělení devíti stejný. Za předpokladu, že n je nenulové číslo, je dán výsledek ciferného sčítání jednoznačně zbytkem po dělení devíti (pokud je číslo dělitelné devíti dostaneme 9, jinak dostaneme přímo zbytek).
Libovolné číslo, které dává po dělení devíti zbytek $z\in\{0,1,2,\ldots,8\}$ můžeme zapsat jako $9c+z$ , kde $c$ je vhodné celé číslo. Tak se to běžně dělá, pro nás ale bude vhodnější volit $z\in\{1,2,\ldots,9\}$ , protože pak $z$ přímo představuje číslo, které dostaneme ciferným sčítáním. Vynásobíme teď dvě různá čísla s různými z:

$(9c_1+z_1)(9c_2+z_2)=9(9c_1c_2+c_1z_2+c_2z_1)+z_1z_2$

Toto myslím chápu.

BrozekP napsal(a):
Na tento součin se podívejme z hlediska toho pravidla.

ciferný součet součinu ciferných součtů činitelů = ciferný součet výsledku.
"Opakovaný" ciferný součet prvního činitele je $z_1$ , "opakovaný" ciferný součet druhého činitele je $z_2$ , zajímá nás tedy "opakovaný" ciferný součet jejich součinu $z_1z_2$ . Tím dostaneme zbytek po dělení $z_1z_2$ devíti (resp. 9 pokud $z_1z_2$ je dělitelné devíti). To samé ale dostaneme, pokud provedeme "opakovaný" ciferný součet pravé strany.

Toto myslím taky, ale nad tím si ještě trochu zapřemýšlím ráno se svěžejší hlavou.

MOC DĚKUJU! Vážně úžasné vysvětlení!

Pavel Brožek · 30. 04. 2010 22:55

↑ Zeus:

Zas to s chválou nepřeháněj, to zdůvodnění by se určitě dalo napsat mnohem srozumitelněji, než jsem byl schopný :-)

PS: Je toto běžný/praktický/pohodlný způsob kontroly výsledku? :-)

Myslím, že ne. Řekl bych, že málokdy potřebuješ násobit velká celá čísla bez použití kalkulačky. A když už potřebuju spočítat součin dvouciferných čísel bez kalkulačky, tak si na to věřím a neověřuji výsledek. Teprve pokud hledám chybu, pak ale raději násobení provedu celé znovu, než abych počítal ciferné součty, které mi v případě chyby stejně neřeknou správný výsledek.

Vlastně jsem tuto zajímavost poprvé viděl jako malý, tuším, že v nějaké encyklopedii edice OKO. Od té doby jsem se s tím nesetkal, až dnes :-)

$n=\sum_{i=0}^{k-1}a_i\cdot (9+1)^i=$\sum_{i=0}^{k-1}a_i$ +9\cdot(\ldots)$

Tady jsem použil binomickou větu. Podrobněji tedy

$\sum_{i=0}^{k-1}a_i\cdot (9+1)^i=\sum_{i=0}^{k-1}a_i$\sum_{j=0}^i{i\choose j}9^j\cdot1^{i-j}$=$

z vnitřní sumy oddělím člen j=0 (to proto, abych ze zbytku mohl vytknout devítku)

$=\sum_{i=0}^{k-1}a_i$1+\sum_{j=1}^i{i\choose j}9^j\cdot1^{i-j}$=\sum_{i=0}^{k-1}a_i$1+9\sum_{j=1}^i{i\choose j}9^{j-1}\cdot1^{i-j}$=\nl =\sum_{i=0}^{k-1}a_i+\sum_{i=0}^{k-1}a_i$9\sum_{j=1}^i{i\choose j}9^{j-1}\cdot1^{i-j}$=\sum_{i=0}^{k-1}a_i+9\sum_{i=0}^{k-1}a_i$\sum_{j=1}^i{i\choose j}9^{j-1}\cdot1^{i-j}$=\nl =\sum_{i=0}^{k-1}a_i+9(\ldots)$

Konstantu tedy můžu ze sumy vytýkat (suma je zde pouze zjednudušení zápisu součtu konečně mnoha sčítanců - z těch přece můžu konstantu vytýkat).

Pokud píšu $9(\cdots)$ , myslím tím, že to je číslo dělitelné devíti. Je to devět krát nějaké libovolné celé číslo, klidně může být zase dělitelné devíti, to už mě nezajímá. Podstatná je ta vytknutá devítka.

S tím $(1+9)^i$ máš pravdu, tam bude vždy zbytek 1.

Pokud jsem něco nezodpověděl, ptej se, v tom množství textu se trochu ztrácím :-)