Matematické Fórum

docasne123 · 01. 05. 2010 14:00

Ahoj chtěl bych vás poprosit o připomenutí základních pravidel pro práci s neznámýma pod odmocninou apod u rovnic a nerovic, poopravit mé dosavadní postupy, ...

1/
$\frac{1}{x} >= 6$
řešení: nemůžu vynásobit "x" protože nevím jestli je kladné či ne, takže převedu na jednu stranu -> společný jmenovatel a udělám tabulku ? Nebo je potřeba dávat pozor na ještě něco ?

2/
$\sqrt{x} + x = 2$
řešení: "x" převedu na druhou stranu a umocním....> kvadratická rovnice a vyjdou dva kořeny (ve výsledcích je jako správný napsaán jen jeden). Je nutné o (ne)rovnic provést kontrolu vždy když provedu umocnění (neekvivalentní úpravu) ?

3/
$x+1 <= \sqrt{x^2+3x}$
Tady nevím, (nebo vím) že bych měl nějak diskutovat velikosti výrazů (pod odmocninou nesmí být záporné číslo 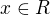$x \in R$ ...) ale vy výsledcích je psáno i diskuse nad "x+1", které přitom není pod odmocninou - proč to tedy diskutovat a jak to vyřešit... ?

4/ rovnice s abs. hodnotou
$|2x-3|=x$
ty základní jako |x-3|=2 umím ale tohle nevím jak si to mám představit pro jako množinu čísel, číslo to bude platit.. (přišel jsem jen na číslo "3"

Kdybyste mi někdo mohl napsat postup velmi "po lopatě" ať to pochopím, byl bych vám vděčný

Díky

halogan · 01. 05. 2010 14:06

↑ docasne123:

1) Z hlediska algoritmického postupu je převod na jednu stranu (anulování) správný, já bych doporučoval trochu zamyšlení. Pokud si to nakreslíš, tak rovnou víš, jaké x bude atp.

2) Ano, zkouška je nutná, protože to je opravdu neekvivalentní úprava. Je to hezky vidět na triviální úloze $\sqrt{x} = -2$ .

3) Pokud bude výraz $x+1$ záporný, tak co nám z toho vyplývá (jaký je vždy výraz na pravé straně)? Pokud je výraz $x+1$ kladný, tak můžeme umocnit, máme na obou stranách nezáporné výrazy.

4) Uměl bys ty křivky nakreslit?

Stýv · 01. 05. 2010 14:13

4) některý rovnice s abs. hodnotou je lepší řešit mechanicky - najdu nulový body, rozdělim si reálnou osu na intervaly dle znamínek výrazů v abs. hodnotě, zbavim se abs. hodnot a řešim obyčejný rovnice

docasne123 · 01. 05. 2010 15:21

1/ díky, nakresleno...
2/ budu si to pamatovat...

4/ díky nakreslil aj zkusil tu tabulku - akorát je to trošku zdlouhavé než člověk všude změní/nezmění znaménka aby vyzkoušel všechny možnosti co jsou v tabulce...

3/ ta mi ale nejde do hlavy... když by byl výraz na pravo přece záporný a stačí jen vlevo zařídit aby $x^2+3x$ byl kladný tak to bude vždycky pravda - akorát nevím jak bo tam vychází kvadratická rovnice => 2 kořeny a ne interval....
když bych přistoupil na tu podmínku že si zjistím že x > -1 (aby byla levá nezáporná), umocním dostanu x > 1 => intervaly spojím takže $x \in <1;+ \infty>$ ale vy výsledku je interval $<-\infty; -3> \cup <1; +\infty)$ . Nevím jak k tomu dojít - mohl byste mi to prosím vysvětlit co mám s čím, jak a proč ?

jarrro · 01. 05. 2010 15:50

$x+1 \leq\sqrt{x^2+3x}$
ak je x+1 záporné a x^2+3*x kladne tak to je pravda teda časť riešenia je interval
$\left(-\infty;-3\right\rangle$
druhá časť riešenia sa nájde umocnením
$x^2+2x+1 \leq x^2+3x\nlx\geq 1$

halogan · 01. 05. 2010 17:19

↑ docasne123:

Není tam kvadratická rovnice, ale kvadratická nerovnice. Nakresli si tu parabolu a uvidíš. Už tedy z předpisu $x^2 + 3x = x(x + 3)$ vidíš, že osu bude protínat v nule a -3, takže odmocnina bude definována na intervalu $(-\infty, -3\rangle \cup \langle 0, \infty)$ . Když to pak zprůnikuješ s tím, kdy je levá strana záporná, tak se dostaneš ke onomu chybějícímu intervalu $(-\infty, -3 \rangle$ .

docasne123 · 01. 05. 2010 18:03

Díky za trpělivost a vysvětlení...

Matematické Fórum

#1 01. 05. 2010 14:00

Principy řešení rovnic a nerovnic - jednoduché

#2 01. 05. 2010 14:06

Re: Principy řešení rovnic a nerovnic - jednoduché

#3 01. 05. 2010 14:13

Re: Principy řešení rovnic a nerovnic - jednoduché

#4 01. 05. 2010 15:21

Re: Principy řešení rovnic a nerovnic - jednoduché

#5 01. 05. 2010 15:50

Re: Principy řešení rovnic a nerovnic - jednoduché

#6 01. 05. 2010 17:19

Re: Principy řešení rovnic a nerovnic - jednoduché

#7 01. 05. 2010 18:03

Re: Principy řešení rovnic a nerovnic - jednoduché

Zápatí