Matematické Fórum

a) kolika způsoby je to možné:

rozdělil bych si to na případy podle počtu žen:

A) 0 žen -> jen 6 chlapů -> nula možností
B) 1 žena -> půjdou všichni chlapi -> můžu ale vybrat  libovolnou ženu -> 4*1
C) 2 ženy -> kolika způsoby mohu vybrat 2 ze 4, když nezáleží na pořadí (to bude 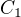); budu potřebovat 5 chlapů -> kolika způsoby můžu vybrat 5 ze 6, když nezáleží na pořadí? (to bude 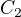) -> počet možných výběrů bude
D) 3 ženy -> obdobně jako C), jen cci vybrat pro 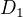3 ze 4, pro 4 ze 6
E) 4 ženy -> obdobně jako C), chci vybrat pro 4 ze 4, pro 3 ze 6


Edit: to B) můžeš řešit jako C) -> 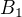chci 1 ze 4, chci 6 ze 6


výsledný počet všech řešení -> A+B+C+D+E

↑ petulkaaa:
jj děkuju moc.. sem si říkala že je to moc složité :)  já nevěděla jestli se to sčítá nebo násobí ! tak děkuju :)