Matematické Fórum

Spybot · 01. 05. 2010 20:56 — Editoval Spybot (02. 05. 2010 16:27)

Automobil s hmotnosťou $m$ sa pohybuje hore miernym kopcom so stúpaním $p$ rýchlosťou $v_1$ . Na spiatočnej ceste dolu kopcom pri rovnakom výkone motora sa automobil pohybuje rýchlosťou $v_2$ .

a) Akou rýchlosťou by sa automobil pohyboval pri rovnakom výkone motora po vodorovnej ceste?

b) Určte výkon motora počas jazdy, ak koeficient trenia má na celej trase hodnotu $f$ .
Úlohu riešte všeobecne a potom pre číselné hodnoty $p = 5 % \,\ v_1 = 60 km/h$ $v_2 = 90 km/h \,\ m = 1 500 kg \,\ f = 0,02 \,\ g = 9,8 m.s^{-2}$ .
Pozn.: Stúpanie $p$ pri danom uhle sklonu $\alpha$ zodpovedá hodnote $tg\alpha$ . Odpor vzduchu proti pohybu vozidla neuvažujte.

Teraz, aby slo auto rovnomerne do kopca, musi platit rovnovaha zlozky tiazovej sily, trecej sily a tahu motora:

$(P=F_mv)$ $F_{m1}=F_t+F_{G1} \Rightarrow \frac{P}{v_1}= fmgcos\alpha+mgsin\alpha$

Dole kopcom je to $F_{m2}+F_{G1}=F_t$ , cize $\frac{P}{v_2}+mgsin\alpha=fmgcos\alpha$ . V zadani je, ze $p=tg\alpha=0.05$ Dalej viem, ze $tg\alpha=\frac{sin\alpha}{cos\alpha} \Rightarrow sin\alpha=pcos\alpha$ , teda vztah vyjadrujuci pohyb dole kopcom upravim na $\frac{P}{v_2}=fmgcos\alpha-mgpcos\alpha=mgcos\alpha\cdot(f-p)$
Ked konfrontujem $(f-p)$ so zadanymi hodnotami, z celeho vztahu potom vyplyva, ze aby auto slo rovnomerne, musi byt sila zaporna, posobit proti smeru pohybu, a teda auto musi brzdit. V zadani je ale spominany len vykon a ten, predpokladam, hybe autom len v smere pohybu. Alebo nie? Co prehliadam?

Vdaka za pomoc.

medvidek · 02. 05. 2010 01:01

↑ Spybot:

Problém zmizne, keď budeš brať rýchlosť 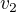$v_2$ ako zápornú.

Dôvod:
Pri zostavovaní rovníc je potrebné stanoviť si akúsi znamienkovú konvenciu. Napr. že sily pôsobiace doprava sú kladné. Podobne i pre rýchlosti. Rovnováha troch síl bude v takom prípade zapísaná vždy rovnako
$F_m+F_t+F_{G1}=0$

Spybot · 02. 05. 2010 17:59

Takze rovnica "dole kopcom" bude vyzerat takto?

Smer vpravo je kladny.

$-F_{m2}-F_{G1}+F_{t}=0 \Rightarrow -\frac{P}{-v_2}-mgsin\alpha+fmgcos\alpha=0$

Spybot · 02. 05. 2010 23:03

Vysledok ma byt $P=2\frac{v_1v_2}{v_1+v_2}fmgcos\alpha\approx 5.9kW$ , nevychadza mi to. Kde robim chybu tentokrat?

medvidek · 03. 05. 2010 04:48

↑ Spybot:
Keď som túto úlohu začal riešiť, zistil som, že jej zadanie je zavádzajúce, až nekorektné.

a)
Pokiaľ by to zadanie končilo bodom a), bolo by všetko v poriadku: Koeficient trenia $f$ nie je známy a nie je známy ani výkon motora $P$ . Vieme, že výkon je rovnaký cestou do kopca i z kopca. Zostavíme dve rovnice pre rovnováhu síl (jednu pre stúpanie, druhú pre klesanie). Vyriešením týchto rovníc sa dopracujeme k vyjadreniu neznámych $P$ a $f$ . No a aby sme mohli odpovedať na otázku a), musíme ešte zostaviť jednu rovnicu pre rovnováhu síl pri vodorovnom pohybe. Dosadíme do nej vypočítané hodnoty $P$ , $f$ a z toho zistíme rýchlosť na vodorovnej ceste.
Mal by si dostať $P=73,4kW$ , $f=0,25$ .

b)
Otázka b) je problematická. Pýta sa vlastne na niečo, čo sme už museli vyriešiť v bode a). To by sa ešte dalo tolerovať, ale je tam napevno daný koeficient trenia. Tým je táto úloha preurčená. Preto ti vyšlo, že pre dané $f=0,02$ musí auto cestou dole kopcom brzdiť. Podmienka rovnosti výkonov teda nie je splniteľná.

Záver:
Vidím, že rovnice pre rovnováhu síl ti nerobia problém :-)
Moja rada na dodržiavanie znamienkovej konvencie bola zbytočná.
Vzťah s výsledkom 5,9 kW nie je správny.

Napíš, ak niečo nie je jasné.

Spybot · 03. 05. 2010 15:42 — Editoval Spybot (03. 05. 2010 15:54)

Tak toto je naozaj zvlastne, tato uloha sa totiz normalne objavila v domacom kole ktorehosi rocnika slovenskej fyzikalnej olympiady. Prikladov odtial som uz preriesil dost a; napriek tomu, ze sa v niektorych objavili drobne chyby, vacsinou len preklepy; este som nenarazil na priklad, ktory by bol "cely zle".

No tentokrat to asi tak bude.
Pri skusobnom dosadeni "vzoroveho" vysledku do ktorejkolvek rovnic to evidentne nevychadza a - v naozaj neposlednom rade - auto s vykonom 5,9 kW (asi 8 koni) je celkom "zaujimave".

No, kazdopadne, ked som to riesil s neznamym koeficientom trenia a mojou povodnou sadou silovych rovnic, vysli mi vysledky, ake aj tebe. Takze to hadam mozme uzavriet.

Vdaka za pomoc a ochotu - po druhykrat.

medvidek · 04. 05. 2010 04:08

↑ Spybot:
Nepodarilo sa mi nikde nájsť túto úlohu i s riešením.
Je to príklad z SK FO - 42. ročník (šk. rok 2000/20011), 1. kolo kategórie D.
Rád som pomohol.

Matematické Fórum

#1 01. 05. 2010 20:56 — Editoval Spybot (02. 05. 2010 16:27)

Jazda automobilu

#2 02. 05. 2010 01:01

Re: Jazda automobilu

#3 02. 05. 2010 17:59

Re: Jazda automobilu

#4 02. 05. 2010 23:03

Re: Jazda automobilu

#5 03. 05. 2010 04:48

Re: Jazda automobilu

#6 03. 05. 2010 15:42 — Editoval Spybot (03. 05. 2010 15:54)

Re: Jazda automobilu

#7 04. 05. 2010 04:08

Re: Jazda automobilu

Zápatí