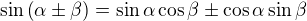Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Laplaceova transformace (TOTO TÉMA JE VYŘEŠENÉ)
#1 04. 05. 2010 01:52
Laplaceova transformace
Ahoj, potřeboval bych od Vás poradit s úpravou zápisu před transformací.
Mám dva obrázky - dvě otázky.
Ten menší obrázek - je tam sin2t = .... mam tento vzor z určitého příkladu brát jako fakt?, nebo jak se k němu došlo přes goniometrické funkce??
a následně jak to bude vypadat pro cos2t
Druhý větší obrázek - tam to chápu všechno až na ten poslední řádek. Kde se vzal najednou cos2... a sin2 ???
Děkuji za odpověď.
Ve čtvrtek jdu na zkoušku a je to pro mě moc důlečité, díky.
Venda
Offline
- (téma jako vyřešené označil(a) gladiator01)
#2 04. 05. 2010 11:59
- gladiator01


- Místo: Jindřichův Hradec
- Příspěvky: 1587
- Škola: ZČU FAV - SWI
- Pozice: absolvent
- Reputace: 53
- Web
Re: Laplaceova transformace
možná  , ale jak se k tomu dostat pomocí vzorců nevím
, ale jak se k tomu dostat pomocí vzorců nevím
Naděje jako svíce jas, potěší srdce štvané, čím temnější je noční čas, tím zářivěji plane.
VIVERE - MILITARE EST (Seneca)
Vím, že nic nevím. - Sokrates
Offline
#3 04. 05. 2010 12:17 — Editoval jelena (04. 05. 2010 12:19)
#9 04. 05. 2010 23:32
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Laplaceova transformace
↑ Vaclav: děkuji, můžeš rovnou dávat odkaz na oblibený materiál, první otázká je tedy v pořádku.
↑ Vaclav: zda se mi to sestaveno a upraveno v pořádku, snažila jsem nepřehlednout znaménka při úpravách, snad se to podařilo.
Jen to značení - "u" - to je zas z jiného materiálu? Děkuji.
Offline
#10 05. 05. 2010 00:19
Re: Laplaceova transformace
↑ jelena:
No můj oblíbený materiál to zrovna není :). Našel jsem ho náhodou, když jsem projížděl zdejší fórum, abych se neptal na něco co je již zodpovězeno.
To značení - "u" - nevim jestli je v nějakým jiným materiaálu, ale takhle to mam v tom jednom příkladu, co jsme dělali o přednášce. Je to taky v nějakejch vypočtenejch příkladech co se počítaj na strojarně v Liberci... - tak to píšu taky tak
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Laplaceova transformace (TOTO TÉMA JE VYŘEŠENÉ)

![kopírovat do textarea $\sin2t\[1\(t-\frac{\pi}{4}\)-1(t-\frac{\pi}{2}\)\]=\sin\(2t\(t-\frac{\pi}{4}\)-2t\(t-\frac{\pi}{2}\)\)=\nl=\sin\(\boxed{2\(t-\frac{\pi}{4}+\frac{\pi}{4}\)\(t-\frac{\pi}{4}\)}-\boxed{2\(t-\frac{\pi}{2}+\frac{\pi}{2}\)\(t-\frac{\pi}{2}\)}\)=$](/mathtex/bd/bdafaff205cdaa2d4bf69c753fa38a9b.gif)