Matematické Fórum

spiderx · 06. 05. 2010 08:02

Dobrý den, mohl by mi někdo pomoct s tímhle - potřeboval bych podrobnější postup, nenašel jsem podobný příklad...

Děkuji za pomoc...

thriller · 06. 05. 2010 09:22

Počítá se to jako dvojný integrál jednotkové funkce přes zadanou plochu, meze integrálu jsou pro x od 0 do 2a, pro y od $\sqrt{(2a)^2-x^2}$ do $\sqrt{a^2-(x-a)^2}$

Rumburak

↑ thriller:
Myslím, že ty meze pro y jsi omylem prohodil, mě aspoň vycházejí od $\sqrt{a^2-(x-a)^2}$ do $\sqrt{(2a)^2-x^2}$ .

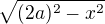↑ spiderx:

Obsah vyšrafovaného obrazce se dá výhodně spočítat jako 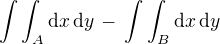$\int \int_A \text{d} x \,\text{d} y \,-\,\int \int_B \text{d} x \,\text{d} y$ ,
kde A je ten čtvtkruh o poloměru 2a , B onen půlkruh o poloměru a . Každý z obou integrálů počítáme zvlášť.
V tom prvním zavedeme polární substituci x = r cos t , y = r sin t , ve druhém x - a = r cos t , y = r sin t .
Meze u prvního i u druhého jistě zvládněš.

thriller · 06. 05. 2010 16:59

↑ Rumburak:
Jo jo, my apologies. Ale výsledek by v absolutní hodnotě vyšel stejně:)

spiderx · 06. 05. 2010 21:50

Podle zadání bych měl použít transformaci do polárek.... ale stejně pořád nevím, jak na to...

Rumburak

↑ spiderx:
"Jak na to" s tím převodem do polárních souřadnic jsem se pokusil naťuknout ve svém předchozím příspěvku, ↑ Rumburak:,
kde jsem poradil vhodné tvary substitučních vzorců. Krom toho je potřeba ještě použít větu o substituci pro dvojný integrál (a podle ní "přepočítat"
do nových souřadnic integrační množinu a integrovanou funkci), v další fázi pak použít Fubiniovu větu. Obojí se dá nalézt i na webu.
Oba integrály v mém odkazovaném příspěvku, na jejichž výpočet jsem úlohu převedl, jsou k dané tematice ty nejjedodušší a při troše vůle
nastudovat a pochopit větu o substituci by s nimi neměl být problém.

Jak konkrerně:
Počítáme integrál 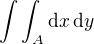$\int \int_A \text{d} x \,\text{d} y$ , kde A je ten čtvtkruh o poloměru 2a.

1.) Je potřeba si zvyknout na to, aby množina, přes kterou se integruje, vždy byla popsána analyticky. Zde takovým popisem bude soustava nerovnic

(1) $x \,\ge\, 0,\,\,y \,\ge\, 0, \,\,x^2 \,+\, y^2 \,\le\,(2a)^2$ ,

které musejí být splněny zároveň. Tedy: bod [x, y] leží v množině A právě tehdy, když jeho souřadnice x, y vyhovují soustavě (1).
(Pokud bychom v této soustavě nahradili neostré nerovnosti odpovídajícími nerovnostmi ostrými, sice by se změnila integrační množina - ubyly by
z ní hraniční body, avšak hodnotu integrálu by taková malá změna neovlivnila).

2.) Popíšeme nyní mnořinu A pomocí polárnárích souřadnic

(2) $x \, = \, r \, \,\cos\, t \,, \, y\, =\, r \,\sin \,t$ .

Přirozenými omezeními zde jsou $r \,>\, 0\,,\,\,t\,\in\,[0, 2\pi)$ , pak má každý bod [x, y] roviny krom [0, 0] jednoznačné vyjádření ve tavru (2)
(že se při tom "nedostane" na bod [0,0] nevadí, při výpočtu integrálu na jednom bodu nesejde). Množinu A obdržíme tím, že (2) dosadíme do (1)
a trochu se nad tím ještě zamyslíme a upravíme to - vznikne tak soustava $0 \,< \,r \le 2a\,,\,\, 0\, \le \,t\le \,\frac {1}{2}\pi$ , která je hledaným popisem množiny A
(krom bodu [0, 0]) v polárních souřadnicích.

3.) Jestliže je za znaménkem integrálu nějaký funkční výraz tvaru f(x,y) , pak substituci (2) provedeme i v něm.

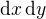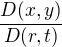4.) "Diferenciální" výraz $\text{d} x \,\text{d} y$ nahradíme výrazem $\|\frac {D(x,y)}{D(r,t)}\|\text{d} r \,\text{d} t$ . Výraz $\frac {D(x,y)}{D(r,t)}$ (v předchozím výraze z něj bereme absolutní hodnotu)
má sice formálně tvar zlomku, avšak není to zlomek, je to tzv. Jacobiho deteminant (slangově Jacobián) pro substituci (2) - jde o determinant sestavený
z parciálních derivací tohoto zobrazení - to už si někde najdi sám .

Tím je substituce provedena.

Co je zde ještě nejasného ?

spiderx · 07. 05. 2010 13:20

↑ Rumburak:

děkuji, tohle se zdá být vyčerpávající. O víkendu nastuduju, uvidím, jestli to půjde. Ještě jednou díky.

Rumburak · 07. 05. 2010 14:54

↑ spiderx:
Ještě poznámka k tomu bodu 2. v předchozím příspěvku (vyjádření možiny A pomocí pol. souřadnic) - potřebuje to dát trochu do pořádku
po formální stránce. Množina A (čtvrtkruh) je od počátku množinou právě všech bodů [x, y] roviny, jejichž souřadnice x, y splňují (1).
Přejdeme-li k polárním souřadnicím, říkáme, že množina A - {[0,0]} je obrazem množiny (již označíme třeba) C, které je množinou včech bodů [r, t] ,
jejichž souřadnice r, t splňují soustavu $0 \,< \,r \le 2a\,,\,\, 0\, \le \,t\le \,\frac {1}{2}\pi$ , což už není (vzhledem k nové soustavě souřadnic) čtvrtkruh, ale obdélník.
"Výstupem" z věty o substituci pak formálně bude integrál přes množinu C (tedy nikoilv již přes množinu A) , takže substitucí náš původní integrál
přejde do tvaru

$\int\int_C \|\frac {D(x,y)}{D(r,t)}\|\text{d} r \,\text{d} t$ .

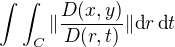To, co jsem psal o substituci do polárních souřadnic, platí obdobně pro kteroukoliv substituci proměnných v integrálu.

Matematické Fórum

#1 06. 05. 2010 08:02

Dvojný integrál a transformace do polárních souřadnic

#2 06. 05. 2010 09:22

Re: Dvojný integrál a transformace do polárních souřadnic

#3 06. 05. 2010 10:16 — Editoval Rumburak (06. 05. 2010 10:18)

Re: Dvojný integrál a transformace do polárních souřadnic

#4 06. 05. 2010 16:59

Re: Dvojný integrál a transformace do polárních souřadnic

#5 06. 05. 2010 21:50

Re: Dvojný integrál a transformace do polárních souřadnic

#6 07. 05. 2010 11:18 — Editoval Rumburak (07. 05. 2010 11:24)

Re: Dvojný integrál a transformace do polárních souřadnic

#7 07. 05. 2010 13:20

Re: Dvojný integrál a transformace do polárních souřadnic

#8 07. 05. 2010 14:54

Re: Dvojný integrál a transformace do polárních souřadnic

Zápatí