Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 08. 05. 2010 17:59 — Editoval Spybot (08. 05. 2010 18:01)
Rovnovaha
Valček s hustotou
, výškou
a hmotnosťou
je zavesený
na jednom konci rovnoramennej páky tak, že jeho os má zvislý smer. Valček je ponorený do hĺbkyvo vode v nádobe s obsahom dna
. Páka je udržiavaná v rovnováhe, t.j. vo vodorovnej polohe, protizávažím s hmotnosťou
, ktoré je zavesené na opačnom konci páky.
a) Určte hmotnosť závažia.
b) O koľko sa posunie hladina vody v pohári, ak zmeníme hmotnosť protizávažia o hodnotu?
Hustota vody je,
. Počas celého deja sa valček nedotýka dna nádoby a voda nevyteká z pohára.
Zaujima ma len cast b, a to pripad kedy protizavaziu znizujeme hmotnost, valec klesa do vody.
Bohuzial, vzorove riesenie so mnou nesuhlasi. Pomozete mi najst chybu v mojom postupe? Uprimna vdaka za pomoc.
Offline
- (téma jako nevyřešené označil(a) Spybot)
#2 08. 05. 2010 19:54
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Rovnovaha
Místo  máš mít
máš mít 
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#3 08. 05. 2010 20:29
Re: Rovnovaha
No, to su tie dva varianty, ako menit hmostnost protizavazia - pridat a ubrat. Ak pridam, valec vystupi z vody a vyjde mi vysledok podla vzoroveho r. Co mi nevychadza je pripad, kedy sa zavaziu hmotnost ubera.
Offline
 )
) Dostanem, comu sa rovna "prirastok ponorenia" valca,
Dostanem, comu sa rovna "prirastok ponorenia" valca, 
 . A zaroven - kedze
. A zaroven - kedze  , valec sa neponori cely.
, valec sa neponori cely. , pricom sa objem vytlacenej vody
, pricom sa objem vytlacenej vody 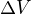 rozleje na plochu
rozleje na plochu 
 Malo by vyjst
Malo by vyjst 