Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 12. 05. 2010 19:06
- docasne123
- Příspěvky: 56
- Reputace: 0
Rovnice s abs. hod.
Ahoj chtěl bych se zeptat jakým postupem se řeší tyto typy rovnic:
1/
jde mi o to jestli do tabulky (doufám že se to přes ní řeší) počítá i s tím "x" napravo, když není v abs. hodnotě a co se pak vlastně dělá s těmi jednotlivými výsledky...
2/ soustava rovnic

Díky moc za pomoc
Offline
- (téma jako vyřešené označil(a) docasne123)
#2 12. 05. 2010 19:45
Re: Rovnice s abs. hod.
↑ docasne123:
2) uděláš substituci ,
,  a řešíš soustavu
a řešíš soustavu
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#3 12. 05. 2010 19:52
- docasne123
- Příspěvky: 56
- Reputace: 0
Re: Rovnice s abs. hod.
Díky to by mě nenapadlo a přitom je to tak elegantní...
Nevíte někdo tu 1/ ?
Offline
#4 12. 05. 2010 19:59 — Editoval da.backer (12. 05. 2010 20:00)
Re: Rovnice s abs. hod.
↑ docasne123:
1)
x dej na levou stranu, udělej nulové body z toho co je JENOM v sbsolutní hodnotě, takže budou 2, to potom dej na osu a vyjdou ti 3 intervaly, POdle nic spočítáš 3 rovnice s příslušným znaménkem (dle intervalu) a nakonec ty 3 rovnice sjednotíš a máš to.
// viz. http://forum.matweb.cz/viewtopic.php?id=17931
Offline
#5 13. 05. 2010 09:00
- docasne123
- Příspěvky: 56
- Reputace: 0
Re: Rovnice s abs. hod.
Díky došel jsem k výsledku třech rovnic a sjednotil s intervaly v nichž jsem počítal... ale třetí rovnice u intervalu od 3 do +nekonečna mi vychází neznamená to, že tato rovnice nemá řešení (ve výsledcích je ale brán naopak celý interval jako správný), nemělo by mi to vyjít
neznamená to, že tato rovnice nemá řešení (ve výsledcích je ale brán naopak celý interval jako správný), nemělo by mi to vyjít  aby to bylo znamenalo že platí celý interval ?
aby to bylo znamenalo že platí celý interval ?
Díky
Offline
#6 13. 05. 2010 09:11 — Editoval Doxxik (13. 05. 2010 09:12)
Re: Rovnice s abs. hod.
o  můžeme prohlásit, že se rovná
můžeme prohlásit, že se rovná  (nula krát cokoli je nula)
(nula krát cokoli je nula)
proto když to dosadíme do nerovnice:  - a to platí vždycky, ne? (kdyžtak si to zanes na osu)
- a to platí vždycky, ne? (kdyžtak si to zanes na osu)
edit: ta tvoje možnost - tak by to muselo být pro  ->
-> 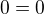
Offline
