Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 14. 05. 2010 18:44
Dukaz aporie
Cus, dneska sem se ucil na maturitu filosofii a dostal sem se k tzn. aporiim coz jsou nejake logicke hadanky ci jak bych toi nazval. Docetl jsem se o aporii Achilles a zelva a bylo zde psano ze v 19. stol byl vymyslen differencialni pocet a tim byla dokazana nesmyslnost teto aporie. Me by ale zajimalo jak :)
Offline
- (téma jako vyřešené označil(a) Krezz)
#3 14. 05. 2010 21:57
Re: Dukaz aporie
↑ Mathe:me jde pouze o ten matematicky dukaz, vim co tim zenon myslel, ale nevim jakou to melo souvislost s differencialnim poctem. V dokumentu ktery sem cetl bylo napsano ze tato aporie byla spochybnena az s objevenim differencialniho poctu a proto by me zajimalo jak. Pokud nekdo vi presne matematicky postup jak to dokozavali tak ho sem napiste nebo poslete odkaz, diky.
Offline
#4 14. 05. 2010 23:07
Re: Dukaz aporie
zenon to vysvětlil nejméně třemi způsoby ale jako matematicky dokázatelny bych si asi vybral ten o půlení trati jelikož nikdy nedojdeš k tomu že by to byla nula a zapsal bych to asi tak to 1/2^n je větší než nula a n je z možiny přirozených čísel
Offline
#5 15. 05. 2010 10:22
Re: Dukaz aporie
↑ Mr.Pinker:Co by byl potom ale vysledek? To bys dokazoval matematickou indukci nebo co stim? Zaroven nerozumim jakou by to potom melo souvislost s diferencialnim poctem. Tohle je docela zapeklite, k mature to samozhrejme nepotrebuju ale zajimalo by me to :)
Offline
#7 15. 05. 2010 10:53 — Editoval Jenda358 (15. 05. 2010 10:57)
Re: Dukaz aporie
Myslím, že je to takto:
Achilles závodí s želvou v běhu na 100 m a je 10krát rychlejší. Želva má zase 10 m náskok.
Achilles uběhne 10 m, želva 1 m. Achilles uběhne 1 m a želva 0,1 m. Achilles 0,1 m a želva 0,01 m. Želva má stále náskok. V jaké vzdálenosti ji tedy Achilles dohoní? To se zjistí součtem jednotlivých úseků, které Achilles uběhl, tedy: 10m + 1 m + 0,1 m + 0,01 m + . . .
To je geometrická řada. Součet členů této řady je 100/9 = 11,111111... m.
Jde tu tedy o to, že nekonečná řada může mít konečný součet.
Offline
#8 15. 05. 2010 11:12 — Editoval Pavel (15. 05. 2010 11:13)
Re: Dukaz aporie
↑ Jenda358:
Je možné to vysvětlit také pomocí doby, za kterou Achilles dohoní želvu.
Nechť se Achilles pohybuje rychlostí 10 m/s a želva 1 m/s a nechť má želva náskok 10m. Achilles uběhne 10 m za 1 sekundu, želva se za tu dobu posune o 1 metr. Ten Achilles uběhne za dalších 0,1 s a za ten čas se želva posune o 10 cm. Tuto vzdálenost dále Achilles uběhne za 0,01 s a želva se za ten čas posune o 1 cm atd. Tzn. aby Achilles dohonil želvu, musí běžet
1 + 0,1 + 0,01 + ... sekundy
To je nekonečná geometrická řada s kvocientem 0,1. Před objevem infinitezimálního počtu nebyl vybudován aparát, jak sčítat nekonečně mnoho kladných čísel. A právě tato aporie je založena na předpokladu, že součet nekonečně mnoha kladných čísel je roven nekonečnu - tzn. Achilles dohoní želvu za nekonečně dlohou dobu. Až s objevem infinitezimálního počtu bylo možno určit součet výše uvedené řady - 10/9 s, tzn. Achilles dohoní želvu v konečném čase.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#10 15. 05. 2010 11:43
Re: Dukaz aporie
↑ Krezz:
Já to znán té verzi, kterou uvádí ↑ Mathe:.
Nesmyslnost nebyla dokázána s objevem dif. počtu. Nesmyslnost byla zjevná už starým Řekům. Oni si ve skutečnosti nemysleli, že by Achiles želvu nedohonil. Oni jen nevěděli, v čem je jejich argumentace chybná.
A chybná byla v to, že si nedokázali představit, že by součet nekonečně mnoha čísel mohl být konečné číslo. A to právě precizoval dif. počet. Zavedl a definoval pojem limity, a pak už to byla hračka.
Takže želva má počáteční náskok  , Achiles rychlost
, Achiles rychlost  , želva rychlost
, želva rychlost  ,
,  a pohybují se po jedné přímce, Achiles honí želvu.
a pohybují se po jedné přímce, Achiles honí želvu.
Než se Achiles dostane do bodu  , potřebuje čas
, potřebuje čas  . ZA tu dobu želva urazí dráhu
. ZA tu dobu želva urazí dráhu 
Nyní A. musí urazit dráhu  za čas
za čas  . A želva
. A želva 
A.  atd.
atd.
Vidíme, že časy tvoří geometrickou posloupnost (ta také byla známa před objevem dif. počtu) a potřebujeme ji sečíst.
Pro G.P. je 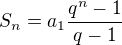 . A tady vstupuje do hry dif. počet, protože potřebuješ vypočítat
. A tady vstupuje do hry dif. počet, protože potřebuješ vypočítat  . Pokud toto matematika zvládá, má takový pojem definovaný a umí s ním zacházet, má vyhráno. To je ale ten problém, protože starořecká matematika (jako celek - někteří jednotlivci se dostali hodně blízko) toto neuměla.
. Pokud toto matematika zvládá, má takový pojem definovaný a umí s ním zacházet, má vyhráno. To je ale ten problém, protože starořecká matematika (jako celek - někteří jednotlivci se dostali hodně blízko) toto neuměla.
Víme, že  ,
, 
Takže "součet" všech časů je  a v tomto čase Achiles dohoní želvu.
a v tomto čase Achiles dohoní želvu.
A světe div se, je to doba, kterou by měl spočítat žák 9. třídy ZŠ, ze zákonů rovnoměrného pohybu. (Achiles se k želvě přibližuje relativní rychlostí  . Za jakou dobu stáhne náskok
. Za jakou dobu stáhne náskok  ?)
?)
Pořádek je pro blbce, inteligent zvládá chaos!
Offline

