Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 16. 05. 2010 15:33
komutující matice
Mám matici: 1 2 0
3 -1 2
0 1 1 A mám najít všechny matice B, tak aby platilo: A.B=B.A.
Tak jedna je určitě jednotková matice a jak najdu ty ostatní? Stačilo by rozepsat to, že bych matici A vynásobila s maticí, která má 9 neznámých (X11,X12,X13,X21,X22,.... ) a na pravé straně to samé a vyjdou mi vlastně na pravé i levé straně stejné vysledky, tak bych řekla, že 9 neznáchých X je z reálných čísel?
Offline
#3 16. 05. 2010 16:14
Re: komutující matice
aha, takže pak mi vznikne soustava o 9 neznámých, takže když mám najít všechny matice B, tak aby bylo A.B=B.A, tak to mi vyjdou jen 2 matice? ta jednotková a druhá, kterou vyřeším ze soustavy?
Nebo nebylo by také možné vypočítat inverzní matici k A (pomocí determinantu a algebraickýho doplnku)?
Offline
#4 16. 05. 2010 16:23
Re: komutující matice
ja som ani neriešiltú sústavu,ale viem,že riešení je nekonečne veľa lebo matica 
pre každé reálne t je dobrá vyriešením sústavy možno prídeš aj na iné možno nie neviem neriešil som
MATH IS THE BEST!!!
Offline
#10 16. 05. 2010 18:31
Re: komutující matice
akože nemá rovnať práveže sa podľa zadania musí rovnať nie 2 riešenia ale nekonečne veľa ako som napísal určite každý reálny násobok jednotkovej matice a neviem či aj iné lebo som sústavu neriešil
MATH IS THE BEST!!!
Offline
#15 16. 05. 2010 19:45 — Editoval BrozekP (16. 05. 2010 19:48)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: komutující matice
Řešit to jako soustavu je jistě možné, ale mně to přijde nezajímavé :-). Co takhle:
Matice A má různá vlastní čísla  (o tom se přesvědčíme výpočtem). Požadujeme
(o tom se přesvědčíme výpočtem). Požadujeme 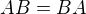 , proto pro každý vlastní vektor
, proto pro každý vlastní vektor 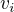 matice A, jemuž přísluší vlastní číslo
matice A, jemuž přísluší vlastní číslo  , platí
, platí .
.
Vektor  je tedy vlastní vektor matice
je tedy vlastní vektor matice  . Protože dimenze podprostoru vlastního čísla
. Protože dimenze podprostoru vlastního čísla  je jedna (každé vlastní číslo matice A je pouze jednonásobným kořenem charakteristického polynomu - v této úloze), je vektor
je jedna (každé vlastní číslo matice A je pouze jednonásobným kořenem charakteristického polynomu - v této úloze), je vektor  násobkem (označme konstantu úměrnosti
násobkem (označme konstantu úměrnosti 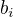 ) vektoru
) vektoru 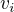 , tedy
, tedy .
.
Matice B má tedy stejné vlastní vektory jako matice A. Snadno už sestrojíme obecnou matici s těmito vlastními vektory a obecnými vlastními čísly 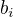 . Dá se také snadno ukázat, že každá takto sestrojená matice už bude splňovat podmínku
. Dá se také snadno ukázat, že každá takto sestrojená matice už bude splňovat podmínku 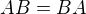 .
.
Vlastní čísla 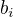 jsou v tomto případě tři, takže dimenze prostoru matic, které vyhovují AB=BA bude tři.
jsou v tomto případě tři, takže dimenze prostoru matic, které vyhovují AB=BA bude tři.
Offline
#16 15. 04. 2012 17:35
- Dalsi Uzivatelske Jmeno

- Příspěvky: 86
- Reputace: 2
Re: komutující matice
↑ jarrro:
Zkouším si tuhle matici vyřešit, něco mi vyšlo, ale teď nevím, co s tím... Tři řádky mi vypadly a zbylo mi tohle:
-2 2 -1 0 2 0 0 0 0 / 0
0 6 -3 -4 0 0 4 0 0 / 0
0 0 -3 0 0 0 4 0 0 /0
0 0 0 1 0 0 0 -3 0 /0
0 0 0 0 1 0 -2 2 -1 /0
0 0 0 0 0 1 0 -2 0 /0
nevím tedy, jestli to je správně, ale kdyby jo, co teď s tím? Když mi v tom posledním řádku zbyly dvě neznámé?
Offline
#18 10. 11. 2012 20:11
- check_drummer

- Příspěvky: 4650
- Reputace: 101
Re: komutující matice
Ahoj, v souvislosti s touto úlohou mám doplňující otázky:
Pavel Brožek napsal(a):
Protože dimenze podprostoru vlastního čísla
je jedna (každé vlastní číslo matice A je pouze jednonásobným kořenem charakteristického polynomu - v této úloze), je vektor
násobkem (označme konstantu úměrnosti
) vektoru
Proč prosím toto platí? Nemůže být vektor  násobkem obecně jiného vektoru
násobkem obecně jiného vektoru  ?
?
Pavel Brožek napsal(a):
Matice B má tedy stejné vlastní vektory jako matice A. Snadno už sestrojíme obecnou matici s těmito vlastními vektory a obecnými vlastními čísly
.
Jakým způsobem bys konstrukci provedl? Mě nenapadá jiná než řešit soustavu 9 rovnic o 9 neznámých...
Díky
"Máte úhel beta." "No to nemám."
Offline
#19 10. 11. 2012 20:24
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: komutující matice
↑ check_drummer:
Ahoj, je vlastní vektor k číslu
je vlastní vektor k číslu  (ukázal jsem
(ukázal jsem  ).
).
Známe vlastně Jordanův rozklad matice B. Z toho už snadno vynásobením tří matic (matice vlastních vektorů, diagonální matice a matice inverzní k matici vlastních vektorů) dostaneme přímo B.
Offline
 vynásob a porovnaj prvok po prvku vynikne sústava a vyrieš ju
vynásob a porovnaj prvok po prvku vynikne sústava a vyrieš ju a pravou stranou nulovou matica sústavy má hodnoť 6 teda nie je tam len nulové riešenie
a pravou stranou nulovou matica sústavy má hodnoť 6 teda nie je tam len nulové riešenie