Matematické Fórum

docasne123 · 18. 05. 2010 11:24

Ahoj,
zanedlouho maturuju z matiky a narazil jsem při počítání na problém...
chtěl bych vás poprosit o radu jak udělat obecnou tečnu ke přímce když má být rovnoběžná s jinou přímkou....
Když mám bod,a tím vést tečnu, tak to zvládnu - vytvořím 1. derivaci a dosadím souřadnice "x" - získám směrnici přímky, takhle ale nevím...
1/ $y=-x^2-4x+8$ tečnu k téhle přímce rovnoběžnou s $p: 4x-2y+7 = 0$
Přemýšlel jsem jestli by to nešlo i nějak přes derivace funkce dané implicitně ?! ale zas nevím jak by to bylo s tím $y^'$

2/ Mohl byste mi někdo jestli je správně tahle derivace ? a jak to lze dále roznásobit ? Rovná se $y*y^'$ něčemu konkrétnímu nebo to vlastně jen napíšu vedle sebe stejně jako $x*y=xy$ ?
$F^'= \frac{x^2y}{y-1} = \frac{(2xy+x^2y^')(y-1)-(x^2y)2(y-1)y^'}{(y-1)^2}$

Díky moc za pomoc

99 · 18. 05. 2010 12:03

2)v te derivacil, jak máš -(x^2*y)*2*(y-1)*y' tak tos asi jen špatně zderivoval ten jmenovatel už s nadruhou místo původní fce, která je y-1, takže tam bude jenom -(x^2*y)*y'

jelena · 18. 05. 2010 12:13

↑ docasne123:

1) opravím zadání: tečna ke křívce $y=-x^2-4x+8$ , tak, že tečná bude rovnoběžná s přímkou $p: 4x-2y+7 = 0$ .

pokud jedna přímka je rovnoběžná s druhou, musí mít stejný normálový vektor, tedy tečná bude mít obecnou rovnici $p: 4x-2y+c = 0$ ,

dosazením $y=\frac{4x-c}{2}.$ do rovnice paraboly hledáme takové c, pro které bude kvadratická rovnice mít pouze jeden kořen (tedy D=0).

2) implicitně zadáná funkce má tvar: $f(x, y)=0$ , proto pokud derivuješ tak, jak je provedeno: $$\frac{x^2y}{y-1}$^{\prime} = \frac{(2xy+x^2y^')(y-1)-(x^2y)y^'}{(y-1)^2}=\boxed{0}$ dostávaš takovou rovnici, ze které lze vyjádřit y´=...

ještě je oprava v derivaci, na závěr čitatele.

Dál už postupuješ stejně, jako v případě tečny k funkci explicitní y=f(x). Materiál

Stačí tak?

Cheop · 18. 05. 2010 12:34 — Editoval Cheop (18. 05. 2010 12:43)

↑ docasne123:
1) $y=-x^2-4x+8=0$
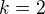2 $4x-2y+7=0\nly=2x+\frac 72$ přímka rovnoběžná s touto přímkou bude mít stejnou směrnici tj: $k=2$ a bude mít tvar:
3) $y=2x+q$
Aby to byla tečna ke křivce $y=-x^2-4x+8=0$ pak přímka a křivka budou mít jeden společný bod.
Rovnici 3) dosadíme do 1) a diskriminant vzniklé kvadratické rovnice bude D = 0 tedy:
$2x+q=-x^2-4x+8\nlx^2+6x+q-8=0\nlD=0\nl6^2-4q+32=0\nl4q=68\nlq=17$
Rovnice tečny je:
$y=2x+17$
Obrázek: