Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 23. 05. 2010 11:53
- matematik123

- Příspěvky: 125
- Reputace: 0
Rotařní kužel
Mám tento příklad
Je-li dán rotační kužel s vrcholem V, S je střed jeho postavy, X libovolný bod podstavné kružnice, platí |SV|=9,2, |úhelSXV|=69|. Vypočítej povrch kužele a udělej náčrt
Náčrt jsem si udělal, ale nevím, jak mám postupovat.
matematik amathér
Offline
#2 23. 05. 2010 11:59 — Editoval frank_horrigan (23. 05. 2010 12:00)
- frank_horrigan


- Příspěvky: 938
- Reputace: 31
Re: Rotařní kužel
Máš výšku kužele a úhel, který svírá strana s podstavou. Použij sinovou větu pro zjištění poloměru podstavy, dál už to zmákneš. Pomohlo?
The only thing worse than being wrong is staying wrong
Sun Tzu - The Art of War
Offline
#3 23. 05. 2010 12:06
- matematik123

- Příspěvky: 125
- Reputace: 0
Re: Rotařní kužel
Jak zní ta věta?
matematik amathér
Offline
#4 23. 05. 2010 12:10 — Editoval frank_horrigan (23. 05. 2010 12:11)
- frank_horrigan


- Příspěvky: 938
- Reputace: 31
Re: Rotařní kužel
↑ matematik123: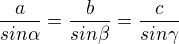
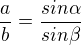 a tak pro všechny strany a úhly trojúhelníku :)
a tak pro všechny strany a úhly trojúhelníku :)
EDIT: něco o sinové větě zde: http://cs.wikipedia.org/wiki/Sinov%C3%A1_v%C4%9Bta
The only thing worse than being wrong is staying wrong
Sun Tzu - The Art of War
Offline
#5 23. 05. 2010 12:13 — Editoval didik (23. 05. 2010 12:29)
Re: Rotařní kužel
Vzorec pro povrch kužele je 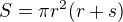
v tomto příkladu platí: 
dále 
Pokud se dobře podíváš do náčrtku zjistíš, že trojúhelník SXV je pravoúhlý s pravým úhlem při vrcholu S.
s pomocí goniometrických funkcí a pythagorovi věty by již neměl být problém spočítat r a s.
PS.: sinová věta není opravdu třeba.
Vím, že nic nevím.
Offline
#6 23. 05. 2010 12:25 — Editoval frank_horrigan (23. 05. 2010 15:49)
- frank_horrigan


- Příspěvky: 938
- Reputace: 31
Re: Rotařní kužel
↑ didik:
Pravděpodobně jde o překlep, 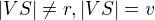 ;)
;)
EDIT: didiku, čoveče, povedlo se ti mně dobře zmagořit :D oprav si ještě ten vzorec pro povrch ;)
The only thing worse than being wrong is staying wrong
Sun Tzu - The Art of War
Offline
#7 23. 05. 2010 12:30
Offline
#8 23. 05. 2010 12:42
- matematik123

- Příspěvky: 125
- Reputace: 0
Re: Rotařní kužel
A kterou goniometrickou funkci mám použít a na co?
matematik amathér
Offline
#9 23. 05. 2010 12:46
- frank_horrigan


- Příspěvky: 938
- Reputace: 31
Re: Rotařní kužel
↑ matematik123:
Víš jak jsou gonio definovaný?? (prilehlá/přepona, protilehlá/přilehlé, atd)??? Tak se podívej na náčrtek, z toho vidíš co je protilehlá, přilehlá, atd a použiješ takovou funkci, která ti dá to co potřebuješ. Stačí se zamyslet, říct "já to vůbec nechápu" je sice fajn, ale nic ti to nedá, když ti to tady spočítáme :)
The only thing worse than being wrong is staying wrong
Sun Tzu - The Art of War
Offline
#10 23. 05. 2010 14:40
- matematik123

- Příspěvky: 125
- Reputace: 0
Re: Rotařní kužel
Nemám výsledek, buď laskav a zkontroluj mi to. Použil jsem tangens 64 stupňou abych zjistil r. protilehlá odvěsna/přilehlá odvěsna. Po úpravě mi vyšlo zaokrouhleně r = 4,5. Pythagorovou větou jsem dopočítal přeponu která mi vyšla 10,24 centimetrou a povrch kužele jsem spočítal pí * r (r+s). Vyšlo mi to 208 centimetrou čtverečbých. Všem zúčastněným tímto srdečně dekuji za součinnost a projevenou náklannost.
matematik amathér
Offline
#11 23. 05. 2010 14:51 — Editoval frank_horrigan (23. 05. 2010 15:48)
- frank_horrigan


- Příspěvky: 938
- Reputace: 31
Re: Rotařní kužel
↑ matematik123:
Máš chybu v opisu zadání, máš mít úhel 69 ne 64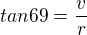
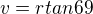
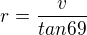


--------------------------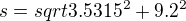
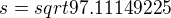
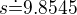
The only thing worse than being wrong is staying wrong
Sun Tzu - The Art of War
Offline
#12 23. 05. 2010 15:39
#13 23. 05. 2010 15:41 — Editoval frank_horrigan (23. 05. 2010 15:48)
- frank_horrigan


- Příspěvky: 938
- Reputace: 31
Re: Rotařní kužel
povrch kužele jsem spočítal pí * r (r+s)
tohle je citace toho postu s tučnou kurzívou ;)
EDIT: jasně, já jsem vůl :) Ano beru zpět a příspevěk edituji :) Děkuji za opravu mé nebetyčné blbosti
The only thing worse than being wrong is staying wrong
Sun Tzu - The Art of War
Offline
#14 17. 06. 2010 16:03
Re: Rotařní kužel
Ahoj mám zadání:
Kužel (r=4cm, v=6 cm) je rozdělen rovinou rovnoběžnou s podstavou na dvě části téhož objemu.
Vypočítejte: a) poloměr kružnice, která je řezem
b) poměr, ve kterém rovina řezu dělí výšku daného kužele.
potřebuji vzorce nebo vysvětlení jak to vypočítat.
Děkuji
Offline