Matematické Fórum

Cheop · 27. 05. 2010 14:02 — Editoval Cheop (27. 05. 2010 14:07)

↑↑ doomed:
Když v čitateli bude pod odmocninou $2+\sqrt3$ tak úpravou opravdu vyjde výsledek $\sqrt2$
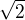
K rozšiřování zlomků:
Obecně to rozšíříš tak, aby Ti ve jmenovatel zmizela odmocnina
a při rozšiřování vhodně využíváš:
$(a+b)(a-b)=a^2-b^2\nl(a\pm b)^2=a^2\pm2ab+b^2$ a podobné úpravy.

gadgetka · 27. 05. 2010 15:07

Jak vhodně zvolit výraz? Stačí si zapamatovat, že $(a-b)(a+b)=a^2-b^2$ ... umocněním odmocnin dostáváš celé číslo a tím pádem jmenovatele bez odmocnin, "vo což tu go". :)

doomed · 27. 05. 2010 16:11 — Editoval doomed (27. 05. 2010 17:04)

Ano, já si tu ale jaksi neuvědomil, že pokud zvolím pro rozšíření výraz $1-\sqrt3$ a pak jej v čitateli při následných úpravách umocním a posléze odmocním, změním tím znaménko celého zlomku, vůbec mě nenapadlo použít výraz $\sqrt3 - 1$ . Já měl za to, že se při volbě vhodného výrazu postupuje podobně jako u komplexních čísel, např. $\frac{1}{1-i} \times \frac{1+i}{1+i}$ , tzn. změním jen znaménko před odmocninou (tedy použiju právě vzorec $a^2 - b^2$ ) a nemusím nad tím přemýšlet (vím, že je to trochu zavádějící přirovnání).

Matematické Fórum

#26 27. 05. 2010 14:02 — Editoval Cheop (27. 05. 2010 14:07)

Re: usměrňování zlomků

#27 27. 05. 2010 15:07

Re: usměrňování zlomků

#28 27. 05. 2010 16:11 — Editoval doomed (27. 05. 2010 17:04)

Re: usměrňování zlomků

Zápatí