Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 27. 05. 2010 20:47
jehlan - výpočet příkladů
1. Vypočtěte obsah podstavy pravidelného pětibokého jehlanu s boční hranou délky 12 cm, je-li její odchylka od roviny podstavy 60°.
2. Podstavou čtyřbokého jehlanu je obdélník s rozměry 24cm a 7cm, průsečík jeho úhlopříček je zároveň patou výšky jehlanu. Vypočtěte objem jehlanu, svírají-li jeho protější boční hrany úhel 106°.
3. Vypočtěte objem pravidelného trojbokého jehlanu, jehož podstava je vepsána do kružnice o poloměru 8 cm a jehož plášť má obsah 147 cm2.
Poradíte mi prosím, jak tyto příklady vypočítat? Vůbec si nevím rady... :(
Offline
- (téma jako vyřešené označil(a) frank_horrigan)
#2 27. 05. 2010 21:04 — Editoval frank_horrigan (27. 05. 2010 21:15)
- frank_horrigan


- Příspěvky: 938
- Reputace: 31
Re: jehlan - výpočet příkladů
1) brali jste goniometrické funkce v pravoúhlém trojúhelníku?? Máš dáno úhel SAV (S je střed opsané kružnice, V je vrchol), délku přepony a když víš, že úsečka SV je kolmá na podstavu, tak máš i pravý úhel. Takže pomocí sinu si spočítej poloměr opsané kružnice - tím budeš mít podstavu rozdělenou na 5 rovnoramenných trojúhelníků, kde každý úhel u středu bude 360/5 = 72°. Tedy v nich máš úhel a délky dvou stran, které jej svírají - > z toho plochu podstavy dopočítáš.
Ostatní zatím vymýšlím, jak pomocí zbraní ZŠ to řešit :)
ad 2) Potřebuješ tedy znát výšku jehlanu. Z vlastností úhlopříček víš, že jsou na sebe kolmé - takže je třeba znát šikmou výšku (hranu) jehlanu. Trochu nechápu co je myšleno tím úhlem 106° - a je to asi dost podstatné, když to máš zadný, ale nevím, jak si to mám nakreslit. Mužeš dodat obrázek, umíš-li si to představit?
ad 3) Potřebuješ znát hranu (jedinou) čtyřstěnu - to by nemusel být problém, namaluj si to dvojrozměrně- jako troúhelník s opsanou kružnicí o daném poloměru - z jejich vlastností pravděpodobně zjistíš délku základny a. Vzorec pro objem čtyřstěnu: 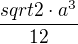 (ber jako fakt) - ten ti odvozovat nebudu, vůbec, na ZŠ se berou objemy čtyřstěnu?
(ber jako fakt) - ten ti odvozovat nebudu, vůbec, na ZŠ se berou objemy čtyřstěnu?
The only thing worse than being wrong is staying wrong
Sun Tzu - The Art of War
Offline
#3 27. 05. 2010 21:18 — Editoval nnnnn (27. 05. 2010 21:33)
Re: jehlan - výpočet příkladů
↑ frank_horrigan:
Díky moc, konečně mi to někdo vysvětlil. Obrázek zachvíli dodám :)
obrázek je tady: http://img4u.net/images/jf2r7mt855rolhj4toh.jpg
Offline
#4 27. 05. 2010 21:34 — Editoval frank_horrigan (27. 05. 2010 21:44)
- frank_horrigan


- Příspěvky: 938
- Reputace: 31
Re: jehlan - výpočet příkladů
↑ nnnnn:
POZOR, řekl jsem ti blbě, pravděpodobně jsi na to přišel/a, ale jenom pro pořádek: ad 1) použiješ COSINUS (60), nebo sinus 30 -což je úhel u vrcholu, ležící proti poloměru)
EDIT: jo, obrázek chápu, zkusím na něco přijít :)
Pomohl strýček gúgl: http://maturita.vlasy.org/Matematika/ma … _rovin.pdf strana 4, písmeno c) Mně pořád uniká, jak si ten úhel mám "shodit" do dvou rozměrů, což obvykle dělávám, když si mám něco představit. Pomohlo aspoň to?
EDIT: není to úplně ono, ale je tam krásně namalováno jak se ten úhel chová u podstavy, z toho už by to mohlo jít
The only thing worse than being wrong is staying wrong
Sun Tzu - The Art of War
Offline
#5 27. 05. 2010 22:12 — Editoval nnnnn (27. 05. 2010 22:17)
Re: jehlan - výpočet příkladů
↑ frank_horrigan:↑ frank_horrigan:
díky, podívám se na to a uvidím, jenom jsem se chtěl zeptat, jak mám dopočítat obsah podstavy v 1, když vím 2 strany a úhel? nějak mi to nedochází...
a v tom 3. příkladu je to trojstěn, ne čtyřstěn nebo ne?
Offline
#6 27. 05. 2010 22:17 — Editoval frank_horrigan (27. 05. 2010 22:19)
- frank_horrigan


- Příspěvky: 938
- Reputace: 31
Re: jehlan - výpočet příkladů
No když víš dvě strany a úhel, dokážeš dopočítat stranu třetí, u rovnoramennýho ještě jednodušeji. 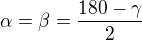 a (třeba) sinová věta, až poznáš třetí stranu tak třeba přes Herona obsah :)
a (třeba) sinová věta, až poznáš třetí stranu tak třeba přes Herona obsah :)
Nebo, mám-li použít nástroje ZŠ, tak z pythagora zjistíš výšku a klasicky obsah :)
Pravidelný trojboký jehlan. Teda podstava je trojúhelník, a ať si to natočíš jakkoli, bude každá stěna stejnou podstavou -> čtyři stěny -> čtyřsten :)
Krychle je taky "čtyřboká", přesto je to šestistěn :)
The only thing worse than being wrong is staying wrong
Sun Tzu - The Art of War
Offline
#7 27. 05. 2010 22:23 — Editoval nnnnn (28. 05. 2010 07:48)
Re: jehlan - výpočet příkladů
Aha, díky, už je mi to jasnější :)
EDIT: Tak jo, myslel jsem, že už to chápu, ale když jsem dopočítal ty první dva příklady, ani na několikátý pokus mi nevyšly... Nevím už jak. Nenapsal bys mi prosím celý postup řešení příkladu?
Offline
#8 28. 05. 2010 11:40 — Editoval frank_horrigan (28. 05. 2010 11:47)
- frank_horrigan


- Příspěvky: 938
- Reputace: 31
Re: jehlan - výpočet příkladů
Rameno trojúhelníku tvořící poloměr opsané kružnice tedy se vzroce 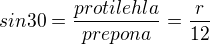 z toho tedy
z toho tedy 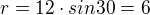 (Sin 30° = 1/2, to snad víš, jednotková kružince nebo "nazpaměť" tabulku s významnými úhly). Úhel u středu jsem ti řekl, 72° , na zbylé dva tedy zbývá 108°, z toho tedy 54° každý. Sinová věta v obecném trojúhelníku zní
(Sin 30° = 1/2, to snad víš, jednotková kružince nebo "nazpaměť" tabulku s významnými úhly). Úhel u středu jsem ti řekl, 72° , na zbylé dva tedy zbývá 108°, z toho tedy 54° každý. Sinová věta v obecném trojúhelníku zní 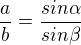 - tedy její derivát (odvozenina). Do rovnice dosadíš a vyjádříš
- tedy její derivát (odvozenina). Do rovnice dosadíš a vyjádříš  (nebo
(nebo  , jde o to jak to máš označený) tedy
, jde o to jak to máš označený) tedy 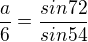
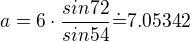
Dosadím do Herona: 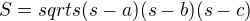
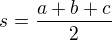
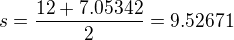

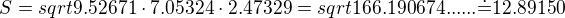
To máš plochu tedy jednoho z pěti shodných trojúhelníků, Takže vynásobíš 5 a máš obsah ( )
)
Skočím se najíst, podívám se si ti pak na ty ostatní
EDIT: jsem rád, že používáš EDIT, ale pozor, není to úplně nejlepší volba ve vyřešeném témtu pokud chceš doplňení po několika hodinách - ono EDIT nerozsvítí vlákno jako nový post, a nemusí si toho nikdo všimnout, já jen že tu mám podobnou úlohu a nechtělo se mi to vymýšlet znova, tak jsem se šel podívat a náhodou si všiml žádosti o doplnění :) Příště za PODOBNÉ situace radši nový příspěvek :)
The only thing worse than being wrong is staying wrong
Sun Tzu - The Art of War
Offline
#9 28. 05. 2010 12:25 — Editoval frank_horrigan (28. 05. 2010 12:34)
- frank_horrigan


- Příspěvky: 938
- Reputace: 31
Re: jehlan - výpočet příkladů
U toho b). ten úhel beta je vlastně úhel rovnoramenného trojúhelníku, jehož ramena jsou výšky "plášťových" torjúhelníků a základna je střední příčka obdélníku (tedy má tu vlastnost, že je stejně dlouhá jako strana a). Takže, jako v minulém případě, máš trojúhelník o základně 24 a úhlech 106,37 a 37 stupňů (z velikosti zadaných proporcí postavy soudím, že by to mohlo odpovídat. Takže: stačí dopočítat plášťovou výšku, opět moje oblíbená sinová věta: 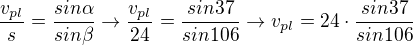
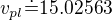
Teď pravoúhlý trojúhelník, odvěsny 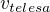 a polovina střední příčky, přeponou budiž
a polovina střední příčky, přeponou budiž  takže pythagoras
takže pythagoras 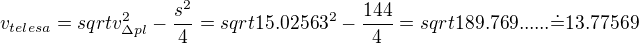
Celý objem jehlanu 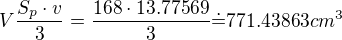
EDIT Postup obecně zpracovaný máš, ty výpočty taky, snad jsou dobře, ale pokud ti to nesedí, tak si to překontroluj nebo to zkus spočítat sám, možná jsem někde udělal numerickou chybu (ale stejně "hezký" čísla nevyjdou, těžko přinutím sinus 106 nebo 72, či kolik to bylo v tom prvním případě být hezký :)
The only thing worse than being wrong is staying wrong
Sun Tzu - The Art of War
Offline
#10 28. 05. 2010 14:53
Re: jehlan - výpočet příkladů
↑ frank_horrigan:
ten první mi taky pořád vychází kolem 65cm2, ale má to vyjít cca 85,5cm2
a ten druhý by měl vyjít kolem 527,5 cm3..
numerickou chybu jsem tam ale zatím nenašel
jinak, díky za radu ohledně EDITU, dám si na to pozor :)
Offline
#12 28. 05. 2010 15:22 — Editoval frank_horrigan (28. 05. 2010 15:30)
- frank_horrigan


- Příspěvky: 938
- Reputace: 31
Re: jehlan - výpočet příkladů
↑ nnnnn:
Jo, jasně :) Chybička se vloudila, opravovat to nebudu, když jsi to odhalil a opravil :)
EDIT: u té 2) taky je možnost využít těch úhlopříček, víš, že se v obdélníku půlí, tedy dokážeš dopočítat délku úhlopříčky (z pythagora) a tedy polovinu snadno. Stačí tedy dopočítat výšku trojúhelníka tvořeného dvěma půlkami úhlopříček a kratší stranou - tím dostaneš délku té "podstavné" odvěsny. Myslel jsem si, že v obdélníku je průsečík středních příček shodný s průsečíkem úhlopříček, ale jak sleduju, že se nedaří, tak asi nejsou (a já si od ZŠ myslel že jo). Zkus to tedy tímto předělaným postupem
The only thing worse than being wrong is staying wrong
Sun Tzu - The Art of War
Offline
#14 02. 03. 2015 13:22
Re: jehlan - výpočet příkladů
Dobrý den,
opět jsem narazil na úlohu: Vypočtěte V pravidelůného pětibokéhojehlanu, znáte-li úhlopříčku podstavy u= 4 cm a boční hranu s= 8 cm.
Vypočítal jsem si výšku v = Odmocnina(8na2 -2na2)=2odmocniny 15. Obsah podstavy pomocí vzorce S=5/8rna2.odmocnina 10+2odmocniny z5= 10,5 cm2 r jsem určil pomocí kosin. věty, r= 2,1 cm
V= 1/3S.v= 27,1 cm3. Může mi někdo potvrdit správnost?
Offline
#15 02. 03. 2015 19:06
- misaH
- Příspěvky: 13467
Re: jehlan - výpočet příkladů
↑ Studanka:
Výpočet výšky sa mi nezdá. Uhlopriečka nejde cez stred podstavy.
Druhý raz si založ vlastnú tému.
Offline
