Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 02. 06. 2010 12:43 — Editoval frank_horrigan (02. 06. 2010 14:06)
- frank_horrigan


- Příspěvky: 938
- Reputace: 31
Vzorové příklady k přijímacím zkouškám (ve výstavbě)
Do tohoto threadu postupně (jak mi čas dovolí) dávat odřešené příklady k příjmačkám na VŠE, s jedním z možných postupů, jak k výsledku dojít (pokud možno nejjednoduším). Udělám to provizorně formou co příspěvek, to jedna z variant, na začátku vždy bude celé zadání (15-ti) příkladů, dále poté jejich řešení, nakonec shrnutí se správnými odpověďmi.
Pokud někdo má námět na vylepšení nebo opravu (můžu udělat chybu, i přesto, že si dám pozor), prosím, diskutujme tyto záležitosti v příslušném vlákně zde: http://forum.matweb.cz/viewtopic.php?id=18852 , kde je i další povídání ohledně tohoto, ke kterému budu rád, pokud se též vyjádříte.
Pro ostatní, převážně tázající platí standradní postup: založit své vlákno, formulovat dotaz, naznačit vlastní řešení a diskutovat postup s kolegy, kteří odpoví
K technickému pozadí: Toto je provizorní řešeni, původně jsem měl na mysli celou samostatnou sekci, kde co thread to faktulta, ovšem kolega Pavel B. nosí v hlavě lepší celkové řešení, proto v průběhu času toto zrealizuje (říkal něco o prázdninách), o čemž poté v tomto tématu budeme viditelně informovat.
Věřím(e), že tento projekt ve své finální fázi usnadní budoucím studentům vysokých škol příjmací zkoušky z matematiky a nám, co zde na fóru působíme ubyde rutinní stále se cyklicky (od dubna do června) opakující se práce:) .
Samozřejmě, toto v žádném případě nemá za úkol potlačit touhu po odpovědi, pokud něčemu konkrétnímu nebudete rozumět - ovšem na stále se opakující stejné dotazy (a velmi podobně formulované) dotazy budiž první odpovědí odkaz sem :)
Přesně ty vzorové příklady, které jsou tedy z loňských testů (ale mám zkušenost s tím, že každou sezonu přijmaček jsou si hodně podobné, jsou ke stažení zde: http://www.vse.cz/download/stahni.php?s … p;lang=cz.
The only thing worse than being wrong is staying wrong
Sun Tzu - The Art of War
Offline
#2 02. 06. 2010 13:10 — Editoval frank_horrigan (03. 06. 2010 15:29)
- frank_horrigan


- Příspěvky: 938
- Reputace: 31
Re: Vzorové příklady k přijímacím zkouškám (ve výstavbě)
VARIANTA A0 zadání
1) Množina všech 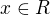 pro která platí
pro která platí  je rovna množině:
je rovna množině:
a) 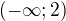 b)
b)  c)
c) 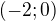 d)
d) 
Řešení:
2) Množina všech
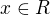 pro která platí
pro která platí  je rovna množině:
je rovna množině:a)
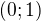 b)
b) 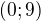 c) prázdná množina d)
c) prázdná množina d) 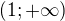
Řešení:
3) Množina všech
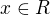 pro která platí
pro která platí  je rovna množině:
je rovna množině:a)
 b)
b)  c)
c) 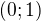 d) prázdná množina
d) prázdná množinaŘešení:
4) Číslo
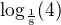 je rovno číslu:
je rovno číslu:a)
 b)
b)  c)
c)  d)
d) 
Řešení:
5) Přímky p1:
 a p2:
a p2:  se protínají uvnitř:
se protínají uvnitř:a) I. kvadrantu b) II. kvadrantu c) III. kvadrantu d) IV. kvadrantu
Řešení:
6) Imaginární část komplexního čísla
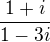 je rovna číslu
je rovna číslua)
 b)
b) 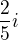 c)
c)  d)
d) 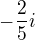
Řešení:
7) Množina všech
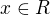 , pro která platí
, pro která platí  je rovna množině:
je rovna množině:a)
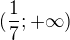 b)
b) 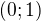 c)
c) 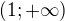 d)
d) 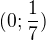
Řešení:
8) Diference aritmetické posloupnosti, ve které platí
 a
a  je rovna číslu:
je rovna číslu:a) 2, b) -2, c) -4, d) 4
Řešení:
9) Číslo
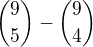 je rovno číslu:
je rovno číslu:a)
 b)
b)  c) 0 d)
c) 0 d) 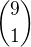
Řešení:
10) Je-li
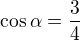 pak číslo
pak číslo  je rovno číslu:
je rovno číslu:a)
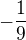 b)
b)  c)
c)  d)
d) 
Řešení:
Těžších 5 příkladů:
11) Množina všech
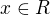 pro která platí
pro která platí  je rovna množině:
je rovna množině:a)
 b)
b) 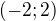 c)
c)  d)
d) 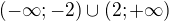
Řešení:
12) Počet všech
 pro která platí
pro která platí  je roven číslu:
je roven číslu:a) 3 b) 2 c) 1 d) 0
Řešení:
13) Reálná část komplexního čísla
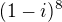 je rovna číslu
je rovna číslua) 16 b) 8 c) -16 d) -8
Řešení:
14) Množina všech
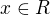 pro která platí
pro která platí  je rovna množině:
je rovna množině:a)
 b)
b)  c)
c)  d)
d) 
Řešení:
15) Množina všech
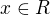 pro která platí
pro která platí  je rovna množině:
je rovna množině:a)
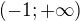 b)
b) 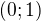 c)
c)  d)
d) 
Řešení:
The only thing worse than being wrong is staying wrong
Sun Tzu - The Art of War
Offline
#3 02. 06. 2010 14:51 — Editoval frank_horrigan (03. 06. 2010 15:30)
- frank_horrigan


- Příspěvky: 938
- Reputace: 31
Re: Vzorové příklady k přijímacím zkouškám (ve výstavbě)
Poznámka: tento postup není úplně striktně matematický, spíš vysvětluju logiku, jakou je možno u zkoušky uplatnit a jakýmkoli způsobem se dobrat cíle. Pokud někdo má lepší vysvětlení, prosím, v příslušném "technickém" vlákně toto zanechte, zde to pak rád odcituji, případně úplně nahradím:)
TODO: (moje poznámky a úkoly)
vymyslet lepší vysvětlení logaritmů o bázi menší než je 1 DONE, pořád to není ono, ale už to vypadá líp, v průběhu času vybrousím
lépe vysvětlit vlastnosti goniofunkcí při přírůstku argumentů
The only thing worse than being wrong is staying wrong
Sun Tzu - The Art of War
Offline
#4 02. 06. 2010 21:10 — Editoval Pavel Brožek (20. 06. 2011 22:56)
Re: Vzorové příklady k přijímacím zkouškám (ve výstavbě)
Takze jelikoz se taky budu ucastnit techto zkousek tak bych rad prispel svym resenim, nehodlam zde vymyslet logicke postupy pokud si to priklad nevynuti a bude se snazit striktne drzet tech mechanickych, matematickych postupu ktere se uci na stredni skole. V planu mam udelat matematicke testy na VSE a taky budu zde psat testy z matematiky na FIT VUT. Pokud by nekdo mel zajem i o jine testy, staci mi napsat na email a test vam zpracuji. Zaroven je zde psano ze se jedna o testy, nebudu zde vsak psat mozne odpovedi, ale ukazu vam jak se k ni dopracovat. Samozhrejme ze pokud mate urcite alternativy na vyber tak se nektere priklady pocitat nemusi a staci postupovat logickou vylucovaci metodou.
Varintu A0 rozpracoval kolega takze zbytek necham na nem.
VSE - Matematika - Varianta A1
1. množina všech reálných čísel, pro která platí  je rovna množině:
je rovna množině:
2. číslo
 je rovno cislu
je rovno cislu3.množina všech reálných čísel pro která platí
 je rovna množině:
je rovna množině:4.číslo
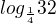 je rovno číslu:
je rovno číslu:5.přímky
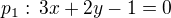 a
a 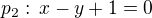 se protínají: (úkolem je určit kvadrant, nikoliv přesnou souřadnici)
se protínají: (úkolem je určit kvadrant, nikoliv přesnou souřadnici)6.imaginární část komplexního čísla
 je rovna číslu:
je rovna číslu:7.množinou všech reálných čísel, pro která platí
 je rovna množině:
je rovna množině:8.sedmý člen
 aritmetické posloupnosti, ve které platí
aritmetické posloupnosti, ve které platí 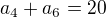 a
a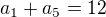 je roven číslu:
je roven číslu:9.množina všech reálných čísel, pro která platí 7^x<-1 je rovna množině:
10. Je-li
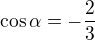 , pak číslo
, pak číslo  je rovno číslu:
je rovno číslu:11.množina všech reálných čísel pro která platí
 je rovna množině:
je rovna množině:12. počet všech
 , pro která platí
, pro která platí 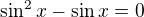 je roven číslu:
je roven číslu:13.reálná část komplexního čísla
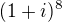 je rovna číslu:
je rovna číslu:14.množina všech reálných čísel, pro která platí
 je rovna množině:
je rovna množině:15.množina všech reálných čísel, pro která platí
 je rovna množíně:
je rovna množíně:Tento test je hotov, máte-li dotazy nebo primoninky vyuzijte topic na ktery odkazuje kolega vyse, nebo smerujte svuj dotaz do sekce středoškolského učiva.
Offline
#5 03. 06. 2010 10:43
Re: Vzorové příklady k přijímacím zkouškám (ve výstavbě)
Varianta E3
Příklady hodnocené pěti body
1) Množina všech reálných čísel. pro která platí  , je rovna. množině:
, je rovna. množině:
2) Podíl
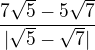 je roven číslu:
je roven číslu:3) Je-lí
 , pak platí:
, pak platí:4) Obecnou rovnici přímky v rovině, která prochází bodem
![kopírovat do textarea $A = [-2,1]$](/mathtex/e4/e4c4ce91fcc6e5cca01ef3409407148c.gif) a je kolmá, k přímce
a je kolmá, k přímce  , lze napsat ve tvaru:
, lze napsat ve tvaru:5) Číslo
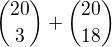 je rovno číslu:
je rovno číslu:6) Je-li
 , pak výraz
, pak výraz  je roven číslu:
je roven číslu:7) Reálná část komplexního čísla
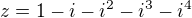 je rovna číslu:
je rovna číslu:8) Množina všech reálných čísel. pro která platí
 , je rovna množině:
, je rovna množině:9) Množina všech reálných čísel, pro která platí
 , je rovna množině:
, je rovna množině:10) Množina všech reálných čísel, pro která platí
 , je rovna množině:
, je rovna množině:Příklady hodnocené deseti body
11) Uvažujme reálnou funkci
 jedné reálné proměnné definovanou předpisem
jedné reálné proměnné definovanou předpisem 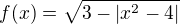 . Určete definiční obor.
. Určete definiční obor.12) Počet všech kořenů rovnice
 , které náleží intervalu
, které náleží intervalu 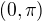 , je roven číslu:
, je roven číslu:13) V rovině je dán trojúhelník o vrcholech
![kopírovat do textarea $A = [3,-4]$](/mathtex/13/1328d29fbf4b0eaa85a608e1bddf5cf2.gif) ,
, ![kopírovat do textarea $B = [2, -1]$](/mathtex/f4/f4f2d3dbbd1ab65b68eead1981f2bf9a.gif) a
a ![kopírovat do textarea $C = [-1, -2]$](/mathtex/ee/ee2650c7ff033431b9844be681481f89.gif) . Poloměr kružnice opsané tomuto trojúhelníku je roven číslu:
. Poloměr kružnice opsané tomuto trojúhelníku je roven číslu:14) Imaginární část komplexního čísla
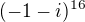 je rovna číslu:
je rovna číslu:15) Všechna řešení rovnice
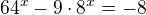 jsou:
jsou:Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#6 03. 06. 2010 20:18 — Editoval frank_horrigan (08. 06. 2010 10:03)
- frank_horrigan


- Příspěvky: 938
- Reputace: 31
Re: Vzorové příklady k přijímacím zkouškám (ve výstavbě)
Varianta A3
1)Množina všech 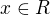 pro která platí
pro která platí  je rovna množině:
je rovna množině:
a)  b)
b) 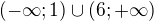 c)
c) 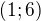 d)
d) 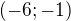
Řešení:
2) Množina všech
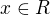 pro která platí
pro která platí  je rovna množině:
je rovna množině:a)
 b)
b) 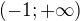 c)
c)  d)
d) 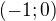
Řešení:
3)Množina všech
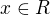 pro která platí
pro která platí  je rovna množině:
je rovna množině:a)
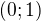 b)
b) 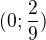 c)
c) 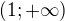 d)
d) 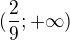
4) Číslo
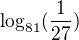 je rovno číslu:
je rovno číslu:a)
 b)
b)  c)
c) 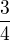 d)
d) 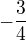
Řešení:
5) Přímky p1:
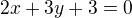 a p2:
a p2: 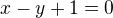 se protínají uvnitř:
se protínají uvnitř:a) I. kvadrantu b) II.kvadrantu c)III.kvadrantu d) IV.kvadrantu
Řešení:
6)Imaginární část komplexního čísla
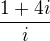 je rovna číslu:
je rovna číslu:a)
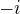 b)
b)  c)
c)  d)
d) 
Řešení:
7) Množina všech
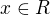 pro která platí
pro která platí  je rovna množině:
je rovna množině:a)
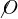 b)
b)  c)
c)  d)
d) 
Řešení:
8) Devátý člen
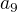 aritmetické posloupnosti, ve které platí
aritmetické posloupnosti, ve které platí 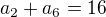 a
a  je roven číslu:
je roven číslu:a) 18 b) 16 c) 15 d) 17
Řešení:
9) Číslo
 je rovno číslu:
je rovno číslu:a)
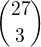 b)
b)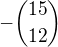 c)
c)  d)
d) 
Řešení:
10) Je-li
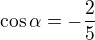 pak číslo
pak číslo  je rovno číslu:
je rovno číslu:a)
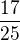 b)
b) c)
c)  d)
d) 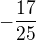
11)Množina všech
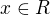 , pro která platí
, pro která platí  je rovna množině:
je rovna množině:a)
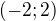 b)
b) 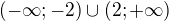 c)
c)  d)
d) 
Řešení:
12) Počet všech
 pro která platí
pro která platí 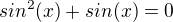 je rovno číslu:
je rovno číslu:a)0 b)1 c)2 d)3
Řešení:
13) Reálná část komplexního čísla
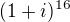 je rovna číslu
je rovna číslua)
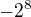 b)
b)  c)
c) d)
d) 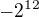
Řešení:
14) Množina všech
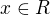 pro která platí
pro která platí  je rovna množině:
je rovna množině:a)
 b)
b)  c)
c)  d)
d) 
Řešení:
15) Množina všech
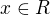 pro která platí
pro která platí  je rovna množině:
je rovna množině:a)
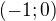 b)
b) 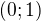 c)
c) d)
d) 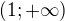
Řešení:
Řešení je podobné jako na variantě A0, proto na stejných příkladech pouze s jinými argumenty napíšu telegraficky postup, tam kde se to liší více to rozvedu :)
The only thing worse than being wrong is staying wrong
Sun Tzu - The Art of War
Offline
#7 04. 06. 2010 14:38 — Editoval jelena (19. 06. 2012 11:44)
Re: Vzorové příklady k přijímacím zkouškám (ve výstavbě)
Varianta F2
Příklady hodnocené pěti body
1. Množina všech reálných čísel, pro která platí  je rovna množině:
je rovna množině:
2. V aritmetìcké posloupnosti plati:
 a
a 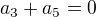 . První člen
. První člen  této
tétoposloupnosti je roven číslu:
3. Výraz
![kopírovat do textarea $\displaystyle\log_3\frac{\sqrt[3]9}{\sqrt{\sqrt[3]3}\cdot\sqrt3}$](/mathtex/cb/cb509862068b2195b8d91b2eeb5aa868.gif) je roven číslu:
je roven číslu:4. Hodnota reálného parametru
 , pro kterou jsou přímky
, pro kterou jsou přímky  a
a 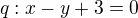 navzájem kolmé, je rovna číslu:
navzájem kolmé, je rovna číslu:5. Počet všech reálných řešení rovnice
 je roven číslu:
je roven číslu:6. Součin
 je roven číslu:
je roven číslu:7. Množina všech reálných čísel, pro která platí
 , je rovna množině:
, je rovna množině:8. Absolutní hodnota komplexního čísla
 je reálné číslo, které je prvkem intervalu:
je reálné číslo, které je prvkem intervalu:9. Množina všech reálných čísel. pro která plat
 , je rovna množině:
, je rovna množině:10. Číslo
 je rovno číslu:
je rovno číslu:Příklady hodnocené deseti body
11. Uvažujme reálnou funkci
 jedné reálné proměnné definovanou předpisem
jedné reálné proměnné definovanou předpisem 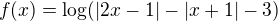 . Definiční obor této funkce je roven množině:
. Definiční obor této funkce je roven množině:12. Počet všech reálných kořenů rovnice
 , které jsou prvky intervalu
, které jsou prvky intervalu  , je roven číslu:
, je roven číslu:13. Imaginámí část komplexního čísla
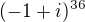 je rovna číslu:
je rovna číslu:14. Uvažujme funkci
 definovanou předpisem
definovanou předpisem 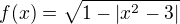 . Definiční obor této funkce je roven množině:
. Definiční obor této funkce je roven množině:15. Obecnou rovnici přímky, která prochází středem kružnice
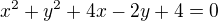 a je kolmá na vektor
a je kolmá na vektor 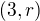 , kde
, kde  je poloměr kružnice, lze napsat ve tvaru:
je poloměr kružnice, lze napsat ve tvaru:Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#8 07. 06. 2010 12:37
Re: Vzorové příklady k přijímacím zkouškám (ve výstavbě)
Varianta G1
Příklady hodnocené pěti body
1. Výraz  je roven číslu:
je roven číslu:
2. Hodnota funkce
 v bodě
v bodě 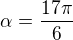 je rovna číslu:
je rovna číslu:3. Množina všech reálných čísel, pro která plati
 , je rovna množině:
, je rovna množině:4. Množina všech reálných čísel, pro která platí
 je rovna množině:
je rovna množině:5. V geometrické posloupnosti je
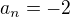 a
a 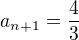 . Pak člen
. Pak člen  této posloupnosti je roven číslu:
této posloupnosti je roven číslu:6. Číslo
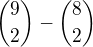 je rovno číslu:
je rovno číslu:7. Počet všech reálných kořenů rovnice
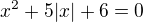 je roven číslu:
je roven číslu:8. Obecnou rovnici přímky v rovině, která prochází bodem
![kopírovat do textarea $[1,2]$](/mathtex/51/51a659b04a172e54a2e9d2711817ba59.gif) a je rovnoběžná s přímkou procházející body
a je rovnoběžná s přímkou procházející body ![kopírovat do textarea $[3, -2]$](/mathtex/8e/8ecd333e7d64a6a0a6401fe7f893e0fe.gif) a
a ![kopírovat do textarea $[-3,2]$](/mathtex/10/10a7a6e31a7d58f80ce1a46d89b3a71b.gif) , lze napsat ve tvaru:
, lze napsat ve tvaru:9. Vzdálenost počátku
![kopírovat do textarea $P = [0;0]$](/mathtex/4c/4c63cf8ebdde41320c5758f8d78e7a00.gif) od středu kružnice
od středu kružnice  je rovna číslu:
je rovna číslu:10. Absolutní hodnota komplexního čísla
 je rovna číslu:
je rovna číslu:Příklady hodnocené deseti body
11. Uvažujme reálnou funkci
 jedné reálné proměnné definovanou předpisem
jedné reálné proměnné definovanou předpisem 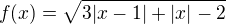 . Definični obor této funkce je roven množině:
. Definični obor této funkce je roven množině:12. Množina všech reálných čísel, pro která platí
 , je rovna množině:
, je rovna množině:13. Imaginární část komplexního čísla
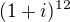 je rovna číslu:
je rovna číslu:14. Počet všech
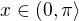 , pro která plati
, pro která plati 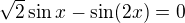 , je roven číslu:
, je roven číslu:15. Uvažujme exponenciální funkci
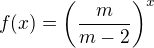 , kde
, kde  je reálná proměnná a
je reálná proměnná a  je reálný parametr. Množina všech hodnot parametrů
je reálný parametr. Množina všech hodnot parametrů  , pro které je uvedená exponenciální funkce klesající, je rovna množině:
, pro které je uvedená exponenciální funkce klesající, je rovna množině:Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#9 08. 06. 2010 10:33 — Editoval frank_horrigan (08. 06. 2010 20:39)
- frank_horrigan


- Příspěvky: 938
- Reputace: 31
Re: Vzorové příklady k přijímacím zkouškám (ve výstavbě)
Varianta A4
1) Množina všech 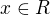 pro která platí
pro která platí  je rovna množině:
je rovna množině:
a) 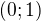 b)
b)  c)
c) 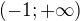 d)
d) 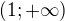
Řešení:
2) Množina všech
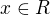 pro která platí
pro která platí  je rovna množině:
je rovna množině:a)
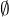 b)
b) 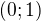 c)
c)  d)
d) 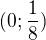
Řešení:
3) Množina všech
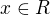 pro která platí
pro která platí  je rovna množině:
je rovna množině:a)
 b)
b) 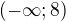 c)
c)  d)
d)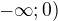
Řešení:
4) Číslo
 je rovno číslu:
je rovno číslu:a)
 b)
b)  c)
c)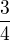 d)
d) 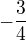
Řešení:
5)Přímky
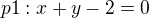 a
a  se protínají uvnitř:
se protínají uvnitř:a) IV. kvadrantu b) II.kvadrantu c) III.kvadrantu d) I.kvadrantu
Řešení:
6) Imaginární část komplexního čísla
 je rovna číslu:
je rovna číslu:a)
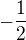 b)
b)  c)
c)  d)
d) 
7)Množina všech
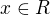 pro která platí
pro která platí  je rovna množině:
je rovna množině:a)
 b)
b)  c)
c)  d)
d) 
8)Diference aritmetické posloupnosti, ve které platí
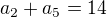 a
a 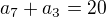 je rovna číslu:
je rovna číslu:a)
 b)
b)  c)
c) 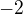 d)
d) 
9)Číslo
 je rovno číslu
je rovno číslua)
 b)
b)  c)
c)  d)
d)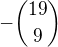
10) Je-li
 pak číslo
pak číslo  je rovno číslu:
je rovno číslu:a)
 b)
b) c)
c)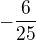 d)
d)
11) Množina všech
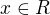 pro která platí
pro která platí  je rovna množině
je rovna množiněa)
 b)
b) c)
c) d)
d)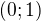
12) Počet všech
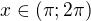 pro která platí
pro která platí 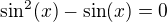 je rovno číslu:
je rovno číslu:a) 2 b) 1 c) 0 d) 4
13) Reálná část komplexního čísla
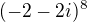 je rovna číslu
je rovna číslua)
 b)
b) c)
c)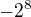 d)
d) 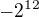
14)Množina všech
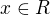 pro která platí
pro která platí  je rovna množině:
je rovna množině:a)
 b)
b)  c)
c)  d)
d) 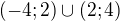
15) Množina všech
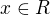 pro která platí
pro která platí  je rovna množině:
je rovna množině:a)
 b)
b) c)
c)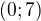 d)
d)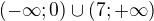
The only thing worse than being wrong is staying wrong
Sun Tzu - The Art of War
Offline
#10 25. 02. 2017 17:14
- Pochopim.cz
- Zelenáč
- Příspěvky: 10
- Škola: různé
- Pozice: Vzdělávací centrum Pochopim
- Reputace: 0
Re: Vzorové příklady k přijímacím zkouškám (ve výstavbě)
Ahoj všichni,
jestli si chcete opakovat na přijímačky z matiky, tak sledujte náš přípravný miniseriál :-)
Odkaz:
http://www.pochopim.cz/prijimaci-zkousk … a-2017.php
Offline

 . Interval nabízený a) tedy ne. Když dosadím 1:
. Interval nabízený a) tedy ne. Když dosadím 1:  ,
,  Tedy interval nabízený b) ano. A protože hned na začátku je psáno, že právě jedna odpověď je správná máme řešení. Záležitost maximálně 1 minuty.
Tedy interval nabízený b) ano. A protože hned na začátku je psáno, že právě jedna odpověď je správná máme řešení. Záležitost maximálně 1 minuty. a na tomto definičním oboru má záporné hodnoty. Z toho snad plyne vše podstatné - interval a)
a na tomto definičním oboru má záporné hodnoty. Z toho snad plyne vše podstatné - interval a) . Dosadim:
. Dosadim: 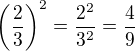 , tedy pořád větší než -1. Záporná mocnina? Zkusme:
, tedy pořád větší než -1. Záporná mocnina? Zkusme:  , tedy pořád kladné. Řešením je prázdná množina, takové x, pro které by nerovnice platila není.
, tedy pořád kladné. Řešením je prázdná množina, takové x, pro které by nerovnice platila není. (tedy není pomalu rostoucí), ale je inverzní k rychle klesající funkci, která má opačný, tedy záporný základ (je typu
(tedy není pomalu rostoucí), ale je inverzní k rychle klesající funkci, která má opačný, tedy záporný základ (je typu  a tedy je pomalu klesající, přesně pravý opak co bylo řešeno výše, log. funkce až do hodnoty argumentu 1 hodně rychle klesá, o osu x se přibrzdí a dál klesá pomalu jak je pro tento typ funkcí typická vlastnost. (logaritmus (1) =0) . Tak, a teď jak na to přijít? Z výše uvedeného už víme, že kladná hodnota to zcela jistě nebude. Tedy připadají do úvahy -2/3 a -3/2. Takže, máme v myšlenkovém procesu započítané tyto věci: Logaritmus se základem menším než 1 se tedy chová podobně jako exponenciální funkce se zápornám základem, v tomto případě má základ -8. Nematematicky řečeno: "stačí graf logaritmu od "klasické" exponenciální funkce obrátit hlavou dolů a zrcadlově dostaneme graf logaritmické funkce od funkce se záporným základem. Takže tedy: aby se hodnota osmičkového logaritmu zvýšila o 1, musel by argument vzrůst 8 krát, a stejně tak to platí i u našeho 1/8-nového: Aby hodnota logaritmu klesla o 1, musel by argument vzrůst 8x. Protože vzrostl "jenom" 4x, bude hodnota zcela jistě v intervalu (-1;0). Na to máme pouze jedno nabízené řešení, c) -2/3
a tedy je pomalu klesající, přesně pravý opak co bylo řešeno výše, log. funkce až do hodnoty argumentu 1 hodně rychle klesá, o osu x se přibrzdí a dál klesá pomalu jak je pro tento typ funkcí typická vlastnost. (logaritmus (1) =0) . Tak, a teď jak na to přijít? Z výše uvedeného už víme, že kladná hodnota to zcela jistě nebude. Tedy připadají do úvahy -2/3 a -3/2. Takže, máme v myšlenkovém procesu započítané tyto věci: Logaritmus se základem menším než 1 se tedy chová podobně jako exponenciální funkce se zápornám základem, v tomto případě má základ -8. Nematematicky řečeno: "stačí graf logaritmu od "klasické" exponenciální funkce obrátit hlavou dolů a zrcadlově dostaneme graf logaritmické funkce od funkce se záporným základem. Takže tedy: aby se hodnota osmičkového logaritmu zvýšila o 1, musel by argument vzrůst 8 krát, a stejně tak to platí i u našeho 1/8-nového: Aby hodnota logaritmu klesla o 1, musel by argument vzrůst 8x. Protože vzrostl "jenom" 4x, bude hodnota zcela jistě v intervalu (-1;0). Na to máme pouze jedno nabízené řešení, c) -2/3 vidíme, že y klesá 2x rychleji než x roste , tedy pro x = 1 bude y = -2. Máme tedy dva body, můžeme načrtnout přímku. Přímka o zadané rovnici bude pouze posunutá po vertikální ose, tedy bude rovnoběžná, takže nakresleme rovnoběžku procházející bodem [0;1]- jak jsme nechali absolutní člen na pokoji, tak přišel čas ho vzít do úvahy. Totéž provedeme s druhou přímkou a oni se nám někde protnou. I pro ty, co neumí moc dobře kreslit bude kvadrant patrný - IV. kvadrant. Pokud chceme řešit analyticky, tak vypočteme soustavu rovnic jak navrhuje kolega níže :)
vidíme, že y klesá 2x rychleji než x roste , tedy pro x = 1 bude y = -2. Máme tedy dva body, můžeme načrtnout přímku. Přímka o zadané rovnici bude pouze posunutá po vertikální ose, tedy bude rovnoběžná, takže nakresleme rovnoběžku procházející bodem [0;1]- jak jsme nechali absolutní člen na pokoji, tak přišel čas ho vzít do úvahy. Totéž provedeme s druhou přímkou a oni se nám někde protnou. I pro ty, co neumí moc dobře kreslit bude kvadrant patrný - IV. kvadrant. Pokud chceme řešit analyticky, tak vypočteme soustavu rovnic jak navrhuje kolega níže :)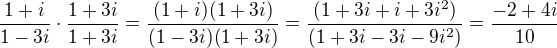 Dál počítat netřeba, je vidět, že bude kladný, ke
Dál počítat netřeba, je vidět, že bude kladný, ke  , jinak pozor na znaménka, nejčastejší chyby, velice často i moje. A pokud dělím dvě komplexní čísla, je třeba si vynásobit "správně mířenou jedničkou, tedy číslem komplexně sdruženým k jmenovateli, to z toho důvodu, aby zmizela imaginární složka ve jmenovateli, pak už se lépe dýchá :)
, jinak pozor na znaménka, nejčastejší chyby, velice často i moje. A pokud dělím dvě komplexní čísla, je třeba si vynásobit "správně mířenou jedničkou, tedy číslem komplexně sdruženým k jmenovateli, to z toho důvodu, aby zmizela imaginární složka ve jmenovateli, pak už se lépe dýchá :) s argumentem
s argumentem  bude 1, logaritmus s argumentem 1 bude 0. Základní fakt, že logaritmus na R není záporný snad nemusím podotýkat. Interval
bude 1, logaritmus s argumentem 1 bude 0. Základní fakt, že logaritmus na R není záporný snad nemusím podotýkat. Interval  . Zjistíme, zda platí i druhá rovnice:
. Zjistíme, zda platí i druhá rovnice:  Takže 4 ta diference nebude, záporná také ne, takže možnost a) platí. Pro zajímavost, podobným postupem:
Takže 4 ta diference nebude, záporná také ne, takže možnost a) platí. Pro zajímavost, podobným postupem: 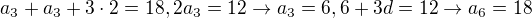 . Sjedeme členy a5 a a2.
. Sjedeme členy a5 a a2. 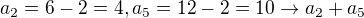 se opravdu
se opravdu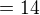
 a
a  budou stejná. Co se stane když odečtu od sebe dvě stejná čísla je jasné žáku druhé třídy ZŠ. Možnost c) 0 bude ta správná. Znovu odkazuji na praci kolegů, kteří vzorečky potvrzující uvádějí, u testů by vám měla stačit znalost této "velmi ořezané verze"
budou stejná. Co se stane když odečtu od sebe dvě stejná čísla je jasné žáku druhé třídy ZŠ. Možnost c) 0 bude ta správná. Znovu odkazuji na praci kolegů, kteří vzorečky potvrzující uvádějí, u testů by vám měla stačit znalost této "velmi ořezané verze" Vyloučeno!
Vyloučeno!
 Vyloučeno, interval končí jako otevřený na -2
Vyloučeno, interval končí jako otevřený na -2 na intervalu
na intervalu  V žádném případě se nic nemění na faktu, že na tomto oboru je funkce sin^2(x) i sin(x) kladná, samotná sin^2 je kladná vždy, zadaná složená funkce umí jít pod nulu díky funkci sin(x), ale až za její půlperiodou. Takže, grafem této složené funkce na příspušném intervalu bude"kopeček" protínající osu x v bodě 0 a bodě pí. Jelikož pí již nenáleží části definičního oboru na kterém máme řešit, zadaná funkce bude rovnat 0 "jenom" právě jednou. Řešení c)
V žádném případě se nic nemění na faktu, že na tomto oboru je funkce sin^2(x) i sin(x) kladná, samotná sin^2 je kladná vždy, zadaná složená funkce umí jít pod nulu díky funkci sin(x), ale až za její půlperiodou. Takže, grafem této složené funkce na příspušném intervalu bude"kopeček" protínající osu x v bodě 0 a bodě pí. Jelikož pí již nenáleží části definičního oboru na kterém máme řešit, zadaná funkce bude rovnat 0 "jenom" právě jednou. Řešení c) 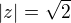 Pomocí Moiverovy věty umocníme:
Pomocí Moiverovy věty umocníme:  . Zkrátíme na základní úhel
. Zkrátíme na základní úhel  Máme tvar
Máme tvar 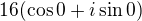 .v Této fázi není třeba nikam už nic převádět, pokud je úhel fí nula nebo 180°, je číslo ryze reálné a tak velké, jak je velká jeho absolutní hodnota, v tomto případě tedy a) 16
.v Této fázi není třeba nikam už nic převádět, pokud je úhel fí nula nebo 180°, je číslo ryze reálné a tak velké, jak je velká jeho absolutní hodnota, v tomto případě tedy a) 16  a jeho opačný ekvivalent. Tedy, jedná se nám o to, zda 1/5 je uvnitř intervalu nerovnice, nebo není. Vyloučit lze možnosti, kdy -1/5 tam patří a 1/5 nikoli a obráceně (řešení a) a b)). Dále z nerovnice je vidět, že nemá ostré je větší/menší, takže je pravděpodobné, že mezní hodnoty tam patřit budou. Výpočtem: Dosaďme tedy za
a jeho opačný ekvivalent. Tedy, jedná se nám o to, zda 1/5 je uvnitř intervalu nerovnice, nebo není. Vyloučit lze možnosti, kdy -1/5 tam patří a 1/5 nikoli a obráceně (řešení a) a b)). Dále z nerovnice je vidět, že nemá ostré je větší/menší, takže je pravděpodobné, že mezní hodnoty tam patřit budou. Výpočtem: Dosaďme tedy za  :
: Nerovnice platí, do intervalu patří. Další vlastnost logaritmů, lze si ji odvodit nakreslením grafu logaritmické funkce, a to že logaritmus o základu a s argumentem převrácené hodnoty a je roven -1.
Nerovnice platí, do intervalu patří. Další vlastnost logaritmů, lze si ji odvodit nakreslením grafu logaritmické funkce, a to že logaritmus o základu a s argumentem převrácené hodnoty a je roven -1.  nula bude krajní mez intervalu. Dosaďme 1:
nula bude krajní mez intervalu. Dosaďme 1: 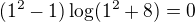 Tedy 1 bude další krajní mez intervalu :)
Tedy 1 bude další krajní mez intervalu :)



![kopírovat do textarea $ 3x+2y-1=0\nl x-y+1=0\nl ..........................\nl 3x+2y-1=0\nl 2x-2y+2=0\nl ..........................\nl 5x+1=0\nl 5x=-1\nl x=-\frac{1}{5}\nl -\frac{1}{5}-y+1=0\nl y=1-\frac{1}{5}\nl y=\frac{4}{5}\nl P[-\frac{1}{5};\frac{4}{5}] $](/mathtex/de/de5991733e4f58b9748f27ccef70c84e.gif)




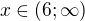

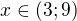

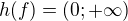








 a zárověň
a zárověň 
 (základ logaritmu je menší než jedna, proto musíme otočit nerovnost) a zárověň
(základ logaritmu je menší než jedna, proto musíme otočit nerovnost) a zárověň 
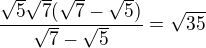

 , pak přímka k ní kolmá procházející bodem
, pak přímka k ní kolmá procházející bodem ![kopírovat do textarea $A[x_0;y_0]$](/mathtex/63/63fb6ceb15daa6f8b7bd2710db5fe273.gif) má rovnici
má rovnici 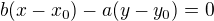 . Dosadíme
. Dosadíme 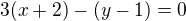 a roznásobíme
a roznásobíme
 a
a 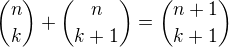
 ,
,
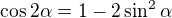 . Dosadíme
. Dosadíme
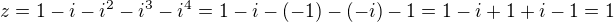
 a zároveň
a zároveň 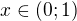
 .
.



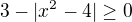
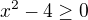 , tj.
, tj. 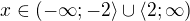
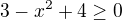

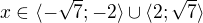
 , tj.
, tj. 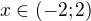
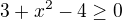
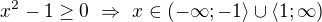


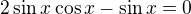
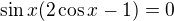
 nebo
nebo 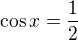
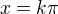 nebo
nebo 
 ) POZOR! Interval je otevřený, takže krajní body oblouku do řešení nepatří.
) POZOR! Interval je otevřený, takže krajní body oblouku do řešení nepatří.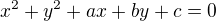 . Dosadíme souřadnice bodů a dostaneme.soustavu
. Dosadíme souřadnice bodů a dostaneme.soustavu ,
, 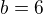 ,
,  . Nyní rovnici
. Nyní rovnici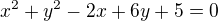 převedeme na středový tvar
převedeme na středový tvar 
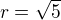
 je pravoúhlý s pravým úhlem u vrcholu
je pravoúhlý s pravým úhlem u vrcholu  . Pak je poloměr kružnice opsané roven polovině přepony
. Pak je poloměr kružnice opsané roven polovině přepony 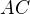 .
.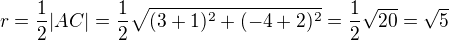
![kopírovat do textarea $[|z|(\cos\alpha+i\sin\alpha)]^n=|z|^n(\cos n\alpha+i\sin n\alpha)$](/mathtex/82/82bddd9308206f04bad324c285e772f3.gif)
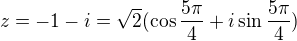
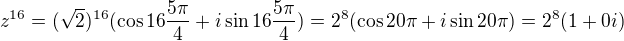

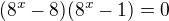
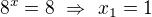
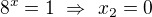

 Dvojka ano
Dvojka ano
 -2 tedy ne
-2 tedy ne




 , tedy i 1 bude součást intervalu, nebude na něm končit. c) vylučuji, b) je správně
, tedy i 1 bude součást intervalu, nebude na něm končit. c) vylučuji, b) je správně . Tedy
. Tedy  a
a 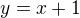 Načrtněme grafy těchto funkcí, už při letmém pohledu vidíme (ti bystřejší i bez načrtnutí) že se protínají ve III. kvadrantu. c)
Načrtněme grafy těchto funkcí, už při letmém pohledu vidíme (ti bystřejší i bez načrtnutí) že se protínají ve III. kvadrantu. c)
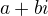 , ta je -1. d) Pozor na znaménka, velmi častá chyba (také je dělám)
, ta je -1. d) Pozor na znaménka, velmi častá chyba (také je dělám)
 Nepovedlo se, vyloučena b)
Nepovedlo se, vyloučena b)



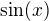 kladných hodnot, obě jsou s půlperiodou
kladných hodnot, obě jsou s půlperiodou  , a protože hledáme průsečíky s osou x, budou dva. Ale protože máme zadaný pouze polouzavřený interval, bude mít zadaná rovnice pouze jeden kořen
, a protože hledáme průsečíky s osou x, budou dva. Ale protože máme zadaný pouze polouzavřený interval, bude mít zadaná rovnice pouze jeden kořen , máme +;+ takžě I. kvadrant, fí 45°
, máme +;+ takžě I. kvadrant, fí 45° . Zpátky převádět netřeba, výsledkem budiž ryze reálné číslo, varianta c)
. Zpátky převádět netřeba, výsledkem budiž ryze reálné číslo, varianta c) 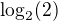 a
a 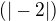 nabývá právě hodnoty 4. Tam je zadáno ostré "menší než", takže 4 do intervalu patřit nebude. d) vyloučeno v první větě, stejně tak c) a b).
nabývá právě hodnoty 4. Tam je zadáno ostré "menší než", takže 4 do intervalu patřit nebude. d) vyloučeno v první větě, stejně tak c) a b). ale
ale 
 , ale
, ale 




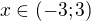
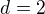 ,
, 
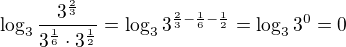
 a
a  . Pokud jsou vektory kolmé, je jejich skalární součin nula.
. Pokud jsou vektory kolmé, je jejich skalární součin nula.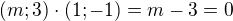
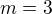
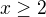
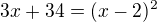
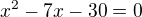

 nebo
nebo 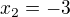 (nevyhovuje podmínce)
(nevyhovuje podmínce) . Argumenty upravíme vhodným odečtením násobků
. Argumenty upravíme vhodným odečtením násobků 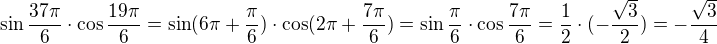
 a zároveň
a zároveň  (základ logaritmu je menší než jedna, proto musíme otočit nerovnost) a zárověň
(základ logaritmu je menší než jedna, proto musíme otočit nerovnost) a zárověň 
 a
a 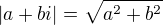 . Je proto
. Je proto 





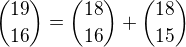 , je hledané číslo
, je hledané číslo 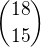 .
. Nerovnici budeme řešit na třech intervalech
Nerovnici budeme řešit na třech intervalech


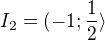






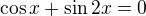
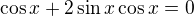
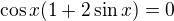
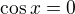 nebo
nebo 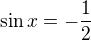
 nebo
nebo 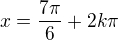 nebo
nebo 
![kopírovat do textarea $(-1+i)^{36}=[(-1+i)^2]^{18}=(1-2i-1)^{18}=(-2i)^{18}=(-2)^{18}i^2=-2^{18}$](/mathtex/25/252a1b02a97b5222e7d6e5a91dbbeb11.gif)
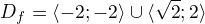


![kopírovat do textarea $S[-2;1]$](/mathtex/5c/5c73853a31ea4c0a44011921656c6f9b.gif) ,
, 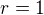
 normálový vektor hledané přímky. Přímka má proto rovnici (podrobněji
normálový vektor hledané přímky. Přímka má proto rovnici (podrobněji 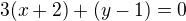

 ,
,  , bude se při odstraňování absolutní hodnoty měnit znaménko.
, bude se při odstraňování absolutní hodnoty měnit znaménko.  znaménko nemění.
znaménko nemění.





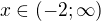



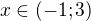

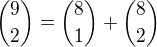 , je
, je 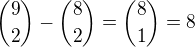
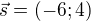 . Její normálový vektor je proto
. Její normálový vektor je proto  .
. a bod přímky
a bod přímky ![kopírovat do textarea $[x_0;y_0]$](/mathtex/c8/c8153ff95e5fc57a75f6a594c9173856.gif) , je rovnice přímky
, je rovnice přímky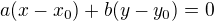 . Dosadíme
. Dosadíme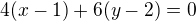 zkrátíme a roznásobíme
zkrátíme a roznásobíme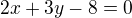
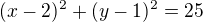 .
. ![kopírovat do textarea $S[2;1]$](/mathtex/10/1067ccdc76174a3ae8647067327cade0.gif) .
.
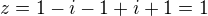
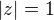
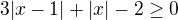 .
. a
a  . Tyto body rozdělí množinu reálných čísel na tři intervaly.
. Tyto body rozdělí množinu reálných čísel na tři intervaly.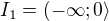
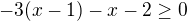

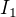 dává
dává 
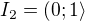
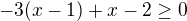
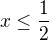
 dává
dává 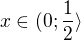
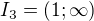
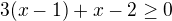


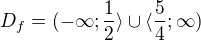
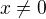



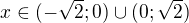
![kopírovat do textarea $(1+i)^{12}=[(1+i)^2]^6=(1+2i-1)^6=2^6i^6=-2^6$](/mathtex/e2/e25f440a7293319c0954a280a9885abb.gif)

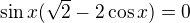
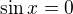 nebo
nebo 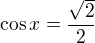

 .
.






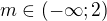


 - odpovídá
- odpovídá
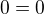 Interval u nuly končí, b) vyloučeno
Interval u nuly končí, b) vyloučeno
 nerovnice tedy platí pro kladná x. d) vyloučeno, a) také, řešením je c)
nerovnice tedy platí pro kladná x. d) vyloučeno, a) také, řešením je c)![kopírovat do textarea $ [\frac13;\frac53]$](/mathtex/22/224962ccc32f822e7ffede63f74b8124.gif)