Matematické Fórum

007Misak · 03. 06. 2010 21:19

ahoj,

potřebuju poradit s pár příkladama k přijímačkám na JČU. Jde o příklady se kterýma prostě nehnu i když vim o všech vzorečkám a podobnejch kravinách ... prostě to sou příklady u kterejch nevim PROČ ... Takže bych byla fakt moc vděčná. Ty příklady si jsou v různejch variantách podobný, takže bych jen potřebovala nakopnout s postupem ...

u 17. bych tak nějak celkově potřebovala poradit, jak poznám všechny křivky, i když si to vždycky převedu na středovou rovnici, tak z toho nic nepoznám ... potřebuju zjistit, podle čeho to mám poznat

u 18. bych taky potřebovala komplet postup...

zdenek1

↑ 007Misak:
20. $f(-2)$ znamená, že do vzorce dosadíš za $x=-2$
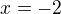
$3^{-2}+\frac1{(-2)^3}=$ a dopočítáš.

Edit: Teď jsem si teprve všimnul, že funkce v př. se jmenuje $h$ a máme počítat $f$ . Takže buďto je tam překlep. nebo něco chybí.

zdenek1

10.
$\log_3(5x+2)-\log_3(2x-1)=1$
$\log_3\frac{5x+2}{2x-1}=\log_33$
$\frac{5x+2}{2x-1}=3$
$5x+2=6x-3$
$x=5$

zdenek1 · 03. 06. 2010 21:34

↑ 007Misak:
1. dosadíš za $x$ a $y$ z rovnice $p$ do rovnice $q$
$1+3t=1+2t+1$
$t=1$
a teď za $t$ dosadíž v rovnici $p$ do $x=1+2t$
$x=1+2=3$

zdenek1 · 03. 06. 2010 21:38

↑ 007Misak:
2. Prostě dosazuj do těch vzorců. Musíš vědět, že průsečík s osou $x$ má $y=0$ . Takže když dosadíš obě hodnoty a v obou ti vyjde nula, je to dobře.
A) pro 0 to vyjde, ale pro 1 ne
B) vyjde pro 0 i 1
C) vyjde pro 1, pro 0 ne
D) nevyjde ani pro jednu možnost
E) vyjde pro 1, pro 0 ne

Správně je tedy B)

easy · 03. 06. 2010 21:43

2)

Jednoduše se pokusíš upravit odpovědi do podoby která ti řekne jejich kořeny ( x(x-a) nebo (x-a)(x-b) )

Autor skryl část textu. Zobrazit/skrýt!

zdenek1 · 03. 06. 2010 21:44

↑ 007Misak:
17.
Díváš se na koeficienty u kvadratický členů
jsou stejné (nenulové) a mají stejné znaménko -> podezření na kružnici
Nejsou stejné (nenulové) a mají stejné znaménko -> podezření na elipsu
Nemají stejné znaménko, můžou, ale nemusí být stejné (nenulové) -> podezření na hyperbolu
Jen jeden kvadratický člen -> podezření na parabolu.
Ve tvém případě: $+1x^2$ a $+4y^2$ koeficienty nejsou stejné a mají stejné znaménko -> podezření na elipsu

Mr.Pinker · 03. 06. 2010 22:05

18
inverzní funkce k
y=1/(1+x)
je tato
x=1/(1+y)
a ted si z toho vyjádříš opět y
x=1/(1+y) \*(1+x)
x+yx=1 \-x
yx=1-x \x
y=(1-x)/x
tudíž bych řekl že E

007Misak · 03. 06. 2010 22:46

děkuju moc ... když mi to někdo takhle vysvětlí, tak to chápu ... což mě samotnou překvapilo :) ještě jednou dík ...

Matematické Fórum

#1 03. 06. 2010 21:19

příklady k přijímačkám na JČU

#2 03. 06. 2010 21:27 — Editoval zdenek1 (03. 06. 2010 22:14)

Re: příklady k přijímačkám na JČU

#3 03. 06. 2010 21:31 — Editoval zdenek1 (03. 06. 2010 21:32)

Re: příklady k přijímačkám na JČU

#4 03. 06. 2010 21:34

Re: příklady k přijímačkám na JČU

#5 03. 06. 2010 21:38

Re: příklady k přijímačkám na JČU

#6 03. 06. 2010 21:43

Re: příklady k přijímačkám na JČU

#7 03. 06. 2010 21:44

Re: příklady k přijímačkám na JČU

#8 03. 06. 2010 22:05

Re: příklady k přijímačkám na JČU

#9 03. 06. 2010 22:46

Re: příklady k přijímačkám na JČU

Zápatí