Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » výpočet limity funkce (TOTO TÉMA JE VYŘEŠENÉ)
#1 27. 03. 2008 22:54
- Slabsí matematik
- Příspěvky: 29
- Reputace: 0
výpočet limity funkce
Ahoj prosim o radu, jiz se zde priklad objevil(od Honza 33, bohuzel se mi nedari se do prispevku pripojit), jedna se o limitu fukce: jdouci k -1
(x^3 +1) / ((sqrt(x^2 -3x) +2x)) lze tedy postupovat podle l´hospitalova pravidla, kdy se zderivuje citatel a jmenovatel. Je asi rozdil derivovat zvlast citatel a zvlast jmenovatel a nebo derivovat funkci jako podil. Ja derivovala zvlast citatel a zvlast jmenovatel. Nevim zda je to spravne
myslim ze postup by mel byt nasledujici: 3x^2 je derivace citatele, a jmenovatel vypada nasledovne 2sqrt ((x-3) * x)/4((sqrt-3)*x) + 2x -3
melo by to vyjit 4
Nejsem si vsak uplne jista postupem, tedy derivaci jmenovatele. Muze prosim nekdo blize rozepsat?
dekuji
Offline
#2 27. 03. 2008 23:15
- robert.marik
- Einstein
- Příspěvky: 999
- Reputace: 1
Re: výpočet limity funkce
derivuje se citatel i jmenovatel zvlast
derivace toho jmenovatele: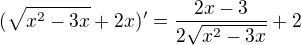
Offline
#3 27. 03. 2008 23:19
- Slabsí matematik
- Příspěvky: 29
- Reputace: 0
Re: výpočet limity funkce
OK diky moc, ten muj jmenovatel ale taky mozna neni uplne spatne ne? Pote uz dosadim pouze za x -1 a dopoctu se k one ctyrce..
Offline
#4 27. 03. 2008 23:42
- robert.marik
- Einstein
- Příspěvky: 999
- Reputace: 1
Re: výpočet limity funkce
no, ja jsem treba nevedel co je (sqrt-3), tak jsem to radsi napsal normalne.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » výpočet limity funkce (TOTO TÉMA JE VYŘEŠENÉ)