Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 08. 06. 2010 11:19
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
goniometrické rovnice
Ahoj, mohl by mě prosím někdo pomoc s příkladem? Nevím jak to mám vypočítat. Děkuji
Příklad: sinx *cosx = 1/2
Offline
- (téma jako vyřešené označil(a) Lucinecka88)
#2 08. 06. 2010 11:26 — Editoval hradecek (08. 06. 2010 11:30)
Re: goniometrické rovnice
Vynásobíš celú rovnicu dvomi...
a už len vyriešiť
Netrápte sa nad svojimi problémami s matematikou, môžem vás uistiť, že tie moje sú ešte väčšie. ~~Albert Einstein~~
Jak spozná člověk, že není pitomec ? - Moudrý člověk to nepozná nikdy a blbci je to jedno. ~~Jak přicházejí básnici o iluze~~
Někteří lidi se nikdy nezmění. Anebo se rychle změní a pak se zase rychle změní nazpátek. ~~Homer Simpson~~
Offline
#4 08. 06. 2010 11:29
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: goniometrické rovnice
↑ hradecek:
kam se ti ztratilo cosx?
Offline
#5 08. 06. 2010 11:31
Re: goniometrické rovnice
↑ Lucinecka88:
Podľa vzorca 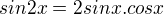
Netrápte sa nad svojimi problémami s matematikou, môžem vás uistiť, že tie moje sú ešte väčšie. ~~Albert Einstein~~
Jak spozná člověk, že není pitomec ? - Moudrý člověk to nepozná nikdy a blbci je to jedno. ~~Jak přicházejí básnici o iluze~~
Někteří lidi se nikdy nezmění. Anebo se rychle změní a pak se zase rychle změní nazpátek. ~~Homer Simpson~~
Offline
#6 08. 06. 2010 11:49
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: goniometrické rovnice
můžu se ještě zeptat na jeden příklad?
sin^2x - sinx = 0
vím že udělám substituci sinx = y, ale jak dál?
Offline
#7 08. 06. 2010 11:51
- teolog


- Místo: Praha
- Příspěvky: 3497
- Škola: MFF + PřF UK
- Pozice: Gymnázium Přírodní škola - učitel (M, Z)
- Reputace: 167
Re: goniometrické rovnice
↑ Lucinecka88:
Když uděláte navrhovanou substituci, tak dostanete rovnici: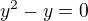
A to je obyčejná kvadratickáá rovnice, doporučuji řešit přes vytknutí.
Offline
#8 08. 06. 2010 11:54
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: goniometrické rovnice
↑ stepan.machacek:
Dobrá, a vyjde mi sinx = 0 a sinx = 1, ta jednička mi vyjde x=90°+K*360° a co ta nula?
Offline
#9 08. 06. 2010 11:58
- teolog


- Místo: Praha
- Příspěvky: 3497
- Škola: MFF + PřF UK
- Pozice: Gymnázium Přírodní škola - učitel (M, Z)
- Reputace: 167
Re: goniometrické rovnice
↑ Lucinecka88:
sinx = 0
x = 0° + k*pí
Offline
#10 08. 06. 2010 12:21
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: goniometrické rovnice
Můžete mi ještě prosím pomoc s tímto? Děkuji
Offline
#11 08. 06. 2010 12:24
#12 08. 06. 2010 12:27
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: goniometrické rovnice
↑ Cheop:
proč ne přes substituci?
Offline
#13 08. 06. 2010 12:34
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: goniometrické rovnice
↑ Lucinecka88:
Protože je to v tomto případě úplně zbytečné.
Nikdo není dokonalý
Offline
#14 08. 06. 2010 13:32
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: goniometrické rovnice
Prosím o pomoc s tímto příkladem děkuji
Offline
#15 08. 06. 2010 13:37 — Editoval hradecek (08. 06. 2010 13:52)
Re: goniometrické rovnice
↑ Lucinecka88:
Zavedieš substitúciu 
a riešiš kvadratickú rovnicu: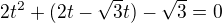
a dopracuješ sa ku koreňom:
dosadíš do substitúcie a máš vyhrané :)))
Netrápte sa nad svojimi problémami s matematikou, môžem vás uistiť, že tie moje sú ešte väčšie. ~~Albert Einstein~~
Jak spozná člověk, že není pitomec ? - Moudrý člověk to nepozná nikdy a blbci je to jedno. ~~Jak přicházejí básnici o iluze~~
Někteří lidi se nikdy nezmění. Anebo se rychle změní a pak se zase rychle změní nazpátek. ~~Homer Simpson~~
Offline
#16 08. 06. 2010 13:42
#17 08. 06. 2010 13:52
Re: goniometrické rovnice
↑ Cheop:Ano, vďaka za poopravenie...výsledky zostávajú tie isté...
Netrápte sa nad svojimi problémami s matematikou, môžem vás uistiť, že tie moje sú ešte väčšie. ~~Albert Einstein~~
Jak spozná člověk, že není pitomec ? - Moudrý člověk to nepozná nikdy a blbci je to jedno. ~~Jak přicházejí básnici o iluze~~
Někteří lidi se nikdy nezmění. Anebo se rychle změní a pak se zase rychle změní nazpátek. ~~Homer Simpson~~
Offline
#18 08. 06. 2010 14:00
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: goniometrické rovnice
Děkuji,ale opravdu nevím jak dál.
Offline
#19 08. 06. 2010 15:10
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: goniometrické rovnice
Udělala jsem toto a nevím jak dál:
Offline
#20 08. 06. 2010 15:33
- teolog


- Místo: Praha
- Příspěvky: 3497
- Škola: MFF + PřF UK
- Pozice: Gymnázium Přírodní škola - učitel (M, Z)
- Reputace: 167
Re: goniometrické rovnice
↑ Lucinecka88:
V tom diskriminantu máte chybu, na konci má být 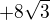 , ale i tak to nevychází moc pěkně.
, ale i tak to nevychází moc pěkně.
Já bych doporučil následující rozklad na součin: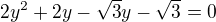
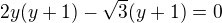
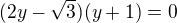
Offline
#22 08. 06. 2010 15:45
Re: goniometrické rovnice
↑ Lucinecka88:
no a ted se vrat zpátky k substituci
sinx= y
a dosad za y výsledky co ti vyšli a dopočítej pro jaké x to je
Offline
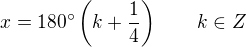
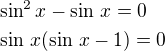
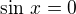
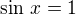
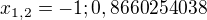
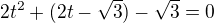 , ale toto:
, ale toto: