Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 07. 06. 2010 10:05
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
exponenciální rovnice 2.
Ahoj, mohl by mě někdo prosím pomoc? Nevím si s tím rady. Děkuji
Offline
- (téma jako vyřešené označil(a) Lucinecka88)
#5 07. 06. 2010 10:41
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: exponenciální rovnice 2.
Děkuji. Má to vyjít -2 a to nevychází.
Offline
#6 07. 06. 2010 10:48
Re: exponenciální rovnice 2.
↑ Lucinecka88:
aby ti vyšlo 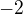 , musíš mít
, musíš mít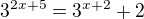
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#7 07. 06. 2010 10:57 — Editoval Lucinecka88 (07. 06. 2010 12:04)
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: exponenciální rovnice 2.
↑ zdenek1:
Omlouvám se, blbě jsem to opsala. Děkuji za upozornění. Ale i tak si s tím nevím rady.
Offline
#8 07. 06. 2010 12:42
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: exponenciální rovnice 2.
Příklad jsem ještě jednou zkusila a vyšlo mi to. Ted si nevím rady s tímto příkladem a prosím o pomoc. Děkuji.
Offline
#9 07. 06. 2010 13:20 — Editoval Cheop (07. 06. 2010 13:37)
#11 07. 06. 2010 13:54
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: exponenciální rovnice 2.
↑ gadgetka:
Můžeš mi prosím vysvětlit dělení 5 na 2?Děkuji
Offline
#12 07. 06. 2010 14:47
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: exponenciální rovnice 2.
To dělení bych celkem chápala,ale další kroky mi jsou nejasné.
Offline
#14 09. 06. 2010 09:22
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: exponenciální rovnice 2.
Ahoj, prosím mohla by jsi mi vysvětlit 8 řádek? Děkuji
Offline

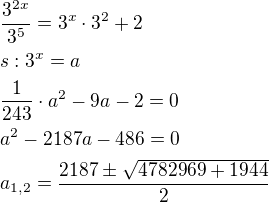
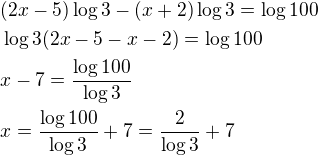

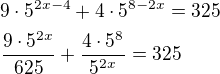
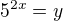
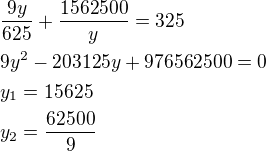
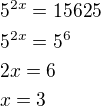


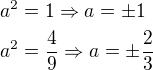
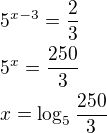
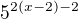
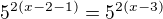
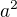 , protože
, protože 